-
Đáp án D
Phương pháp: phân tích
Cách giải:
Đầu năm 1930, với sự ra đời của Đảng Cộng sản Việt Nam (từ tháng 10-1930) đã mở ra thời kì mới của cách mạng ở Đông Dương. Sau đó, Đảng cộng sản đã khẳng định được vị trí lãnh đạo của mình, đưa cách mạng Đông Dương phát triển, giành được nhiều thắng lợi trong cuộc kháng chiến chống Pháp và chống Mĩ
Câu hỏi:Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = a\sqrt 3 ,AD = AA' = a\), O là giao điểm của AC và BD. Thể tích khối chóp OA’B’C’D’ là x, Thể tích khối chóp OBB’C’ là y. Tính giá trị x+y.
- A. \(x + y = \frac{{5{a^3}\sqrt 3 }}{8}\)
- B. \(x + y = \frac{{5{a^3}\sqrt 3 }}{4}\)
- C. \(x + y = \frac{{7{a^3}\sqrt 3 }}{12}\)
- D. \(x + y = \frac{{5{a^3}\sqrt 3 }}{12}\)
Đáp án đúng: D
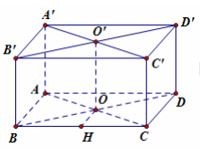
Gọi \(O' = A'C' \cap B'D' \Rightarrow OO' = a\)
\(\Rightarrow {V_{OA'B'C'D'}} = \frac{1}{3}OO'.{S_{A'B'C'D'}} = \frac{{{a^3}\sqrt 3 }}{3} = x\)
Vẽ \(OH \bot BC \Rightarrow OH = \frac{{a\sqrt 3 }}{2}\)
\(\Rightarrow {V_{OBB'C'}} = \frac{1}{3}OH.{S_{BB'C}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{1}{2}a.a = \frac{{a\sqrt 3 }}{{12}} = y\)
Từ đó suy ra \(x + y = \frac{{5{a^3}\sqrt 3 }}{{12}}.\)
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ TÍNH THỂ TÍCH KHỐI ĐA DIỆN BẰNG CÁCH TRỰC TIẾP
- Cho hình lăng trụ ABCD.A' B' C' D' có đáy ABCD là hình vuông cạnh a các cạnh bên tạo với đáy một góc 60 A’ cách đều các đỉnh A,B,C,D
- Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh bên bằng AA’=3a và đường chéo AC’=5a
- Từ một mảnh giấy hình vuông cạnh là 4 cm, người ta gấp nó thành bốn phần đều nhau rồi dựng lên thành bốn mặt xung quanh của hình hình lăng trụ tứ giác đều như hình vẽ
- Tính thể tích V của lăng trụ đứng tam giác có độ dài các cạnh đáy là 37 cm; 3 cm; 30 cm và biết tổng diện tích các mặt bên là 480 cm^2
- Tìm thể tích lớn nhất của hình hộp chữ nhật ABCD.A’B’C’D’ có tồng diện tích của tất cả các mặt là 36, độ dài đường chéo AC’ bằng 6
- Tính thể tích V của khối lăng trụ có đáy là tam giác đều cạnh a, có cạnh bên bằng b, góc giữa cạnh bên và mặt đáy bằng 60^0.
- Tính thể tích của khối đa diện đều có các đỉnh là trung điểm các cạnh của một tứ diện đều cạnh a
- Tính theo a tích của khối lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằnga, hình chiếu vuông góc của A’ lên mặt phẳng (ABC) là trung điểm H của cạnh AB
- Tính thể tích V khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa SB với mặt phẳng (ABCD) bằng 60 độ
- Vật thể nào trong các vật thể sau không phải là khối đa diện






