-
Câu hỏi:
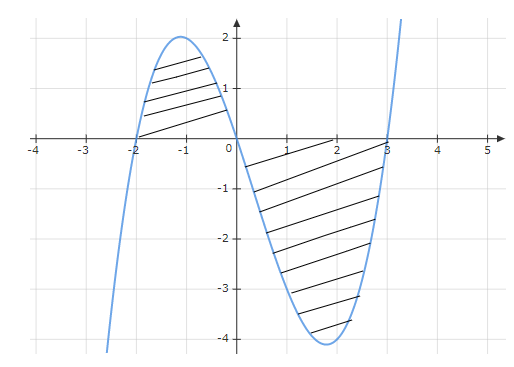
Cho đồ thị hàm số y = f(x). Xác định công thức tính diện tích S của hình phẳng (phần gạch chéo) trong hình.
- A. \(S = \int\limits_{ - 2}^3 {f\left( x \right)dx}\)
- B. \(S = \int\limits_0^{ - 2} {f\left( x \right)dx} + \int\limits_2^3 {f\left( x \right)dx}\)
- C. \(S = \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_3^0 {f\left( x \right)dx}\)
- D. \(S = \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx}\)
Lời giải tham khảo:
Đáp án đúng: C
Nhìn vào đồ thị ta thấy \(f\left( x \right) \ge 0\) với \(x \in \left[ { - 2;0} \right]\) \(\Rightarrow {S_1} = \int\limits_{ - 2}^0 {f\left( x \right)dx}\)
\(f\left( x \right) \le 0\) với \(x \in \left[ {0;3} \right]\)
\(\Rightarrow {S_2} = \int\limits_3^0 {f\left( x \right)dx}\)
Vậy C là đáp án đúng.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho đồ thị hàm số y = f(x). Xác định công thức tính diện tích S của hình phẳng (phần gạch chéo) trong hình
- Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^4} - 5{x^2} + 4\), trục hoành và hai đường thẳng \(x = 0;x = 1\).
- Tính diện tích S của hình phẳng giởi hạn bởi đồ thị hàm số \(y = x^3 - x\) và đồ thị hàm số \(y = {x^2} - x.\)
- Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = 0;x = \pi\), biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x\left( {0 \le x \le \pi } \right)\) là một tam giác đều có cạnh là \(2\sqrt {\sin x}\).
- Tính thể tích V của khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường \(y = \frac{4}{{x - 4}},y = 0,x = 0,x = 2\) quay một vòng quanh trục Ox là (theo đơn vị thể tích).
- Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm
- Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(x^3 - x\) và đồ thị hàm số \(y = x - x^2\)
- Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = (x -1)e^{2x}\) ,trục tung và đường thẳng y = 0.
- Diện tích hình phẳng giới hạn bởi \(y = x^2 - x + 3\) và \(y = 2x + 1\) là:
- Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = \sqrt x \) và y = 6 - x và trục tung là: