Phương pháp giải bài toán lực đàn hồi, lực hồi phục môn Vật Lý 12 năm 2021-2022

a) Lực đàn hồi

Lực đàn hồi là lực của lò xo tác dụng vào các vật gắn vào hai đầu của lò xo.

- Phương: Lực đàn hồi có phương trùng với trục của lò xo.

- Chiều: Lực đàn hồi có chiều ngược với chiều biến dạng của lò xo. Nếu lò xo dãn ra, lực đàn hồi có chiều ngược lại chiều dãn của lò xo. Nếu lò xo bị nén, lực đàn hồi có chiều dãn ra.

- Độ lớn: Độ lớn của lực đàn hồi bằng tích của độ cứng và độ biến dạng của lò xo với chiều dài tự nhiên.

\({{F_{hh}} =  - k\left| {\Delta l} \right| =  - k\left| {\left( {l - {l_0}} \right)} \right|}\)

Trong đó, k là độ cứng của lò xo (N/m), l là chiều dài của lò xo ở vị trí đang xét,  là chiều dài tự nhiên của lò xo (m).

Biểu thức đại số:

\({{F_{hh}} =  - k\Delta l =  - k\left( {l - {l_0}} \right)}\)

Dấu trừ biểu thị lực đàn hồi luôn có chiều ngược với chiều biến dạng của lò xo.

a) Lực hồi phục

Lực hồi phục trong con lắc lò xo là hợp lực tác dụng vào vật (không tác dụng vào điểm treo).

- Phương: Lực hồi phục có phương trùng với trục của lò xo.

- Chiều: Lực hồi phục có chiều ngược với chiều li độ của vật, tức là có chiều luôn hướng về vị trí cân bằng của vật.

- Độ lớn: Độ lớn của lực hồi phục bằng tích của độ cứng và li độ của vật.

\({{F_{hp}} = k\left| x \right|}\)

Trong đó, k là độ cứng của lò xo (N/m), x là li độ của vật (m).

Biểu thức đại số:

\({{F_{hp}} =  - kx}\)

Dấu trừ biểu thị lực hồi phục luôn có chiều ngược với chiều li độ. Hay lực hồi phục ngược pha với li độ.

* Trường hợp lò xo nằm ngang

Trong trường hợp lò xo nằm ngang thì độ biến dạng của lò xo chính bằng độ lớn li độ x của vật. Như vậy, trường hợp này thì lực đàn hồi và lực hồi phục có độ lớn bằng nhau, và bằng \(k\left| x \right|\).

- Độ lớn cực đại của lực đàn hồi cũng như lực hồi phục là kA.

- Độ lớn cực tiểu của lực đàn hồi cũng như lực hồi phục là 0.

Về giá trị, vì \(-A\le x\le A\) nên \(-kA\le {{F}_{hp}}=-kx=-k\Delta l\le kA\)

Suy ra:

- Lực hồi phục (cũng như lực đàn hồi) cực đại là kA khi vật ở biên âm.

- Lực hồi phục (cũng như lực đàn hồi) cực tiểu là –kA khi vật ở biên dương.

* Trường hợp lò xo thẳng đứng

(1) Chiều dài lò xo

Gọi \({{l}_{0}}\) là chiều dài tự nhiên của lò xo, \({{l}_{cb}}\) là chiều dài khi con lắc ở vị trí cân bằng và \(\Delta {{l}_{0}}\) là độ dãn của lò xo khi vật ở vị trí cân bằng thì ta có

Gọi A là biên độ của con lắc khi dao động.

Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng xuống dưới. Chiều dài của lò xo khi vật ở vị trí có li độ x bất kì là \(l={{l}_{0}}+\Delta {{l}_{0}}+x\)

Vì \(-A\le x\le A\) nên ta có \(\left\{ \begin{align} & {{l}_{\max }}={{l}_{0}}+\Delta {{l}_{0}}+A \\ & {{l}_{\min }}={{l}_{0}}+\Delta {{l}_{0}}-A \\ \end{align} \right.\)

Từ đây ra rút ra biểu thức quen thuộc \({{l_{\max }} - {l_{\min }} = 2A}\)

(2) Lực đàn hồi

Độ lớn lực đàn hồi khi vật ở vị trí có li độ x trong con lắc lò xo thẳng đứng xác định bởi công thức

\({{F_{hh}} = k\left| {l - {l_0}} \right| = k\left| {\Delta {l_0} + x} \right|}\)

- Độ lớn cực đại của lực đàn hồi

Vì \(x \le A\) nên lực đàn hồi có độ lớn cực đại là \(\left( {\Delta {l_0} - A} \right)\)

- Độ lớn cực tiểu của lực đàn hồi

\({{F_{hh\,\min }} = k\left| {\Delta {l_0} - A} \right| = k\left| {\Delta {l_0} - A} \right|}\)

Nếu \(\Delta {l_0} \le A\) thì độ biến dạng nhỏ nhất của lò xo là , suy ra độ lớn cực tiểu của lực đàn hồi là \({F_{hh\,\min }} = 0\)

Trong trường hợp này, lò xo luôn luôn dãn, lực đàn hồi là lực kéo.

Nếu \(\Delta {l_0} \le A\) thì độ biến dạng nhỏ nhất của lò xo là 0, do đó độ lớn cực tiểu của lực đàn hồi là

Trong trường hợp này, lò xo có lúc nén, có lúc dãn.

- Lực nén xuất hiện khi vật ở vị trí thỏa mãn \(\left| x \right| > \Delta l\) (xem hình vẽ), có độ lớn xác định bởi

\({F = k\left( {\left| x \right| - \Delta l} \right)}\)

Lực nén cực đại \({{F_{\max }} = k\left( {A - \Delta l} \right)}\)

Hình bên trái ứng với trường hợp \(\Delta {{l}_{0}}>A\), hình bên phải ứng với trường hợp \(\Delta {{l}_{0}}

Lò xo nén khi vật đi từ vị trí \(x=-\Delta {{l}_{0}}\) theo chiều âm đến vị trí \(x=-\Delta {{l}_{0}}\) theo chiều dương. Gọi \({{\varphi }_{ne\grave{u}n}}\) là góc quét được trên đường tròn khi lò xo nén. Dựa vào đường tròn, ta có \({{\varphi }_{ne\grave{u}n}}=2\alpha \) 

Trong đó: \(\cos \varphi =\frac{\Delta {{l}_{0}}}{A}\)

- Thời gian lò xo nén trong một chu kì là \({{t}_{ne\grave{u}n}}=\frac{{{\varphi }_{ne\grave{u}n}}}{\omega }\)

- Thời gian lò xo dãn trong một chu kì là \({{t}_{da\tilde{o}n}}=\frac{{{\varphi }_{da\tilde{o}n}}}{\omega }=\frac{2\pi -{{\varphi }_{ne\grave{u}n}}}{\omega }=T-{{t}_{ne\grave{u}n}}\)

Ví dụ 1: Trong quá trình dao động, chiều dài của con lắc lò xo treo thẳng đứng biến thiên từ 30 cm đến 50 cm. Khi lò xo có chiều dài 40 cm thì

A. tốc độ của vật cực đại. 

B. gia tốc của vật cực đại.

C. lực phục hồi tác dụng vào vật bằng với lực đàn hồi.

D. pha dao động của vật bằng 0.

Lời giải

Ta có \({{l}_{\text{max}}}-{{l}_{\min }}=2A\Rightarrow A=10\,\,\text{cm}\).

Mặt khác, \({{l}_{\max }}={{l}_{0}}+\Delta {{l}_{0}}+A\Rightarrow {{l}_{0}}+\Delta {{l}_{0}}={{l}_{\max }}-A=40\,\,\text{cm}\)

Chiều dài của lò xo tại vị trí có li độ x là \({{l}_{x}}={{l}_{0}}+\Delta {{l}_{0}}+x\).

Khi \({{l}_{x}}=40\) thì \(x={{l}_{x}}-\left( {{l}_{0}}+\Delta {{l}_{0}} \right)=40-40=0\).

Suy ra vật đang ở vị trí cân bằng, tốc độ cực đại.

Đáp án A.

Ví dụ 2: Con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể. Hòn bi đang ở vị trí cân bằng thì được kéo xuống dưới theo phương thẳng đứng một đoạn 3 cm rồi thả nhẹ cho nó dao động. Hòn bi thực hiện 50 dao động mất 20 s. Cho \(g={{\pi }^{2}}=10\,\text{m/}{{\text{s}}^{\text{2}}}\). Tỉ số độ lớn lực đàn hồi cực đại và cực tiểu của lò xo khi dao động là

A. 7.                                   B. 5.                                   C. 4.                                   D. 3.

Lời giải

Hòn bi đang ở vị trí cân bằng thì được kéo xuống dưới theo phương thẳng đứng một đoạn 3 cm rồi thả nhẹ nên biên độ \(A=3\text{ cm}\).

Hòn bi thực hiện 50 dao động mất 20 s nên tần số

\(f=\frac{N}{t}=\frac{50}{20}=2,5\,\text{Hz}\Rightarrow \omega =2\pi f=5\pi \,\left( \text{rad/s} \right)\)

Độ biến dạng của lò xo khi vật nằm ở vị trí cân bằng

\(\Delta {{l}_{0}}=\frac{g}{{{\omega }^{2}}}=\frac{10}{{{\left( 5\pi  \right)}^{2}}}=\frac{10}{250}=0.04\,\text{m}=4\,\text{cm}\)

- Vì \(A<\Delta {{l}_{0}}\) nên trong quá trình dao động lò xo luôn dãn

-  Lực đàn hồi có độ lớn cực đại khi vật xuống thấp nhất \(F_{\tilde{n}h}^{\max }=k\left( \Delta {{l}_{0}}+A \right)\)

- Lực đàn hồi có độ lớn cực tiểu khi vật lên cao nhất \(F_{\tilde{n}h}^{\min }=k\left( \Delta {{l}_{0}}-A \right)\)

Vậy tỉ số cần tìm là \(\frac{F_{\tilde{n}h}^{\max }}{F_{\tilde{n}h}^{\min }}=\frac{k\left( \Delta {{l}_{0}}+A \right)}{k\left( \Delta {{l}_{0}}-A \right)}=\frac{\Delta {{l}_{0}}+A}{\Delta {{l}_{0}}-A}=\frac{4+3}{4-3}=7\)

Đáp án A.

Ví dụ 3: Con lắc lò xo treo thẳng đứng, vật nặng treo ở phía dưới lò xo dao động với biên độ \(A=12\text{ cm}\). Biết tỉ số giữa lực cực đại và lực cực tiểu của lò xo tác động lên vật là 4. Độ dãn của lò xo khi vật ở vị trí cân bằng là

A. 10 cm.                           B. 12 cm.                           C. 15 cm.                           D. 20 cm.

Lời giải

Vì theo bài ra ta có \(\frac{F_{\tilde{n}h}^{\max }}{F_{\tilde{n}h}^{\min }}=4\ne \infty \Rightarrow F_{\tilde{n}h}^{\min }\ne 0\) tức là lò xo luôn bị dãn khi vật dao động.

Khi vật xuống thấp nhất, độ biến dạng của lò xo lúc đó là lớn nhất nên

\(F_{\tilde{n}h}^{\max }=k\left| \Delta {{l}_{0}}+A \right|\)

Khi vật lên cao nhất, độ biến dạng của lò xo lúc đó là nhỏ nhất nên

\(F_{\tilde{n}h}^{\min }=k\left| \Delta {{l}_{0}}-A \right|\)

Theo bài ra \(\frac{F_{\tilde{n}h}^{\max }}{F_{\tilde{n}h}^{\min }}=\frac{k\left( \Delta {{l}_{0}}+A \right)}{k\left( \Delta {{l}_{0}}-A \right)}=4\Rightarrow \Delta {{l}_{0}}=\frac{5A}{3}=20\,\,\text{cm}\)

Đáp án D.

Ví dụ 4: Một con lắc lò xo treo thẳng đứng. Kích thích cho vật dao động (được móc ở phía dưới của lò xo) dao động điều hòa theo phương thẳng đứng với chu kì 0,4 s và biên độ 8 cm. Chọn \({x}'x\) thẳng đứng, chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian là lúc vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do \(g=10\,\text{m/}{{\text{s}}^{\text{2}}}\). Thời gian ngắn nhất kể từ thời điểm ban đầu đến lúc lực đàn hồi của lò xo có độ lớn cực tiểu là

A. \(\frac{7}{30}\,\,\text{s}\text{.}\)                        

B. \(\frac{1}{30}\,\,\text{s}\text{.}\)           

C. \(\frac{3}{30}\,\,\text{s}\text{.}\)                             

D. \(\frac{4}{15}\,\,\text{s}\text{.}\)

Lời giải

Nhớ lại cách tính thời gian, ta cần xác định vị trí đầu và vị trí cuối của chuyển động. Vị trí ban đầu thì rõ rồi, vật đi qua vị trí cân bằng theo chiều dương. Vị trí lúc sau là vị trí lực đàn hồi có độ lớn cực tiểu, ta cần phải biết được \(\Delta {{l}_{0}}\) lớn hơn hay nhỏ hơn A.

Ta có

\(\Delta {{l}_{0}}=\frac{mg}{k}=\frac{g}{{{\omega }^{2}}}=\frac{{{T}^{2}}g}{4{{\pi }^{2}}}=\frac{0,{{4}^{2}}.10}{4.10}=0,04\,\text{m}=4\,\text{cm}=\frac{A}{2}\)

Do đó \(\Delta {{l}_{0}}

Thời gian cần tìm là thời gian vật đi từ vị trí cân bằng theo chiều dương, đến biên dương rồi từ biên dương đến vị trí \(-\frac{A}{2}\) theo chiều âm.

Dựa vào đường tròn, ta tính được góc quét lúc này là \(\frac{7\pi }{6}\) nên thời gian là

\(\Delta t=\frac{7}{30}\text{s}\)

Đáp án A. 

Ví dụ 5: Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với chu kì 1,2 s. Trong một chu kì, nếu tỉ số của thời gian lò xo dãn với thời gian lò xo nén bằng 2 thì thời gian mà lực đàn hồi ngược chiều lực kéo về là

A. 0,2 s.                             B. 0,1 s.                             C. 0,3 s.                             D. 0,4 s.

Lời giải

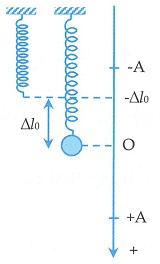
- Chọn chiều dương hướng xuống.

- Trong quá trình dao động của vật, lò xo có nén nên \(\Delta l

- Theo bài ra, ta có \(\frac{{{t}_{da\tilde{o}n}}}{{{t}_{ne\grave{u}n}}}=\frac{T-{{t}_{ne\grave{u}n}}}{{{t}_{ne\grave{u}n}}}=2\Rightarrow {{t}_{ne\grave{u}n}}=\frac{T}{3}\)

- Trong khoảng thời gian \(\frac{T}{3}\), lò xo bị nén khi vật chuyển động từ vị trí có li độ \(x=-\Delta l\) theo chiều âm, đến biên âm, rồi từ biên âm trở về vị trí \(x=-\Delta l\) theo chiều dương. Góc quét được của chất điểm tương ứng trên đường tròn là \(\frac{2\pi }{3}\).

Sử dụng đường tròn dễ dàng suy ra \(\Delta l=\frac{A}{2}\)

 - Lực kéo về luôn hướng về VTCB, lực đàn hồi là lực đẩy nếu lò xo nén, lực kéo nếu lò xo dãn.

- Từ đó, ta có nhận xét: trong 1 chu kì, thời gian lực đàn hồi ngược chiều với lực kéo về gồm:

+ Thời gian vật đi từ vị trí cân bằng theo chiều âm đến vị trí có li độ \(x=-\Delta l=-\frac{A}{2}\) theo chiều âm

+ Thời gian vật đi từ vị trí có li độ \(x=-\Delta l=-\frac{A}{2}\) theo chiều dương đến vị trí cân bằng theo chiều dương

- Vậy thời gian cân tính là \(\frac{T}{12}+\frac{T}{12}=\frac{T}{6}=0,2\text{s}\)

.Nếu ta không biết vì sao có nhận xét trên, thì ta có thể giải thích như sau. Vì lực đàn hồi ngược chiều lực hồi phục nên tích giá trị đại số của chúng là một số âm.

Ta có

\(\left\{ \begin{align} & {{F}_{hp}}=-kx \\ & {{F}_{\tilde{n}h}}=-k\left( \Delta l+x \right) \\ \end{align} \right.\Rightarrow {{F}_{hp}}.{{F}_{\tilde{n}h}}<0\Leftrightarrow kx.k\left( \Delta l+x \right)<0\Leftrightarrow -\Delta l\)

Đáp án A.

Ví dụ 6: Một con lắc lò xo treo thẳng đứng xuôi, vật nhỏ \(m=100\text{ gam}\) và lò xo có khối lượng không đáng kể. Chọn gốc tọa độ ở VTCB, chiều dương của hệ trục hướng lên. Biết vật dao động theo phương trình \(x=4\cos \left( 10t-\frac{2\pi }{3} \right)\). Lấy \(g=10\,\text{m/}{{\text{s}}^{\text{2}}}\). Tìm độ lớn lực đàn hồi và lực phục hồi tác dụng vào vật tại thời điểm vật đã đi được quãng đường \(S=3\text{ cm}\) kể từ lúc bắt đầu dao động.

A. 0,1 N và 0,9 N.            

B. 0,9 N và 0,1 N.            

C. 0,2 N và 0,8 N.            

D. 0,8 N và 0,2 N.

Lời giải

Vì lực đàn hồi có độ lớn \(\left| {{F}_{\tilde{n}h}} \right|=k\Delta l\) và \(\left| {{F}_{hp}} \right|=k\left| x \right|\) nên để tính chúng, ta cần tìm k và phải biết được sau khi vật đi được 3 cm thì vật đến điểm nào để từ đó biết nó cách vị trí cân bằng bao nhiêu (độ lớn li độ bằng bao nhiêu) và lúc đó lò xo dãn bao nhiêu (độ dãn của lò xo so với chiều dài tự nhiên)

Độ cứng \(k=m{{\omega }^{2}}=0,{{1.10}^{2}}=10\text{ N/m}\)

Độ dãn của lò xo khi vật ở VTCB:

\(\Delta {{l}_{0}}=\frac{g}{{{\omega }^{2}}}=\frac{10}{{{10}^{2}}}=\frac{10}{100}=0,1\,\,\text{m}=10\,\,\text{cm}\)

Dựa vào đường tròn thấy ngay thời điểm ban đầu vật có li độ \(x=-2\,\text{cm}\) và đang đi theo chiều dương.

Hoặc ta có thể thay t=0 vào phương trình x, v ta có ngay trạng thái ban đầu 

\(\left\{ \begin{align} & {{x}_{0}}=-2\,\,\text{cm} \\ & {{v}_{0}}>0 \\ \end{align} \right.\)

Dựa vào đường tròn, sau khi đi được quãng đường \(S=3\text{ cm}\) thì vật đến tọa độ \(x=1\,\text{cm}\), lúc đó lò xo bị dãn một đoạn

\(\Delta l=\Delta {{l}_{0}}-\left| x \right|=10-1=9\,\,\text{cm}\)

Vậy lực phục hồi và lực đàn hồi có độ lớn là 

\(\left\{ \begin{align} & {{F}_{hp}}=kx=10.0,01=0,1\left( N \right) \\ & {{F}_{\tilde{n}h}}=k\Delta l=10.0,09=0,9\left( N \right) \\ \end{align} \right.\)

Đáp án A.

Ví dụ 7: Gọi M, N, I là các điểm trên một lò xo nhẹ, được treo thẳng đứng ở điểm O cố định. Khi lò xo có chiều dài tự nhiên thì \(OM=MN=NI=10\,\text{cm}\). Gắn vật nhỏ vào đầu dưới I của lò xo và kích thích để vật dao động điều hòa theo phương thẳng đứng. Trong quá trình dao động tỉ số độ lớn lực kéo lớn nhất và độ lớn lực kéo nhỏ nhất tác dụng lên O bằng 3; lò xo dãn đều; khoảng cách lớn nhất giữa hai điểm M và N là 12 cm. Lấy \({{\pi }^{2}}=10\). Vật dao động với tần số là:

A. 2,9 Hz.                       

B. 2,5 Hz.                         

C. 3,5Hz.                          

D. 1,7Hz.

Lời giải

Vì khoảng cách lớn nhất giữa M và N là 12 cm, tức là độ dài đoạn MN lớn nhất bằng 12 cm. Mà độ dài đoạn MN ban đầu là 10 cm, suy ra độ dãn lớn nhất của lò xo giới hạn bởi hai đầu MN là \(12-10=2\text{ cm}\).

Vì lò xo dãn đều và ban đầu \(OM=MN=NI\) nên ở mọi thời điểm, OM, MN và NI luôn có độ dài bằng nhau. Suy ra độ dãn của chúng ở mọi thời điểm cũng bằng nhau. Vậy độ dãn lớn nhất của lò xo là \(\Delta {{l}_{\text{max}}}=3.2=6\,\text{cm}\).

Mà ta có \(\frac{{{F}_{\max }}}{{{F}_{\min }}}=\frac{k\Delta {{l}_{\max }}}{k\Delta {{l}_{\min }}}=\frac{\Delta {{l}_{\max }}}{\Delta {{l}_{\min }}}=3\Rightarrow \Delta {{l}_{\min }}=\frac{6}{3}=2\,\text{cm}\)

Vậy \(\Delta l=\frac{\Delta {{l}_{\max }}+\Delta {{l}_{\min }}}{2}=4\,\text{cm}\).

Suy ra \(f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}=\frac{1}{2}\sqrt{\frac{g}{{{\pi }^{2}}\Delta l}}=\frac{1}{2}\sqrt{\frac{10}{10.0,04}}=2,5\,\text{Hz}\).

Đáp án B.

Câu 1: Trong một dao động điều hòa của con lắc lò xo thì:

A. Lực đàn hồi luôn khác 0.                                       

B. Lực hồi phục cũng là lực đàn hồi.

C. Lực đàn hồi bằng 0 khi vật qua VTCB.                 

D. Lực phục hồi bằng 0 khi vật qua VTCB.

Câu 2: Trong dao động điều hòa của con lắc lò xo, lực gây nên dao động của vật là:

A. Lực đàn hồi.                                                            

B. Có hướng là chiều chuyển động của vật.

C. Có độ lớn không đổi.   

D. Biến thiên điều hòa cùng tần số với tần số dao động riêng của hệ dao động và luôn hướng về vị trí cân bằng.

Câu 3: Tìm phát biểu đúng khi nói về con lắc lò xo?

A. Lực đàn hồi cực tiểu của con lắc lò xo khi vật qua vị trí cân bằng.

B. Lực đàn hồi của lò xo và lực phục hồi là một.

C. Khi qua vị trí cân bằng lực phục hồi đạt cực đại.

D. Khi đến vị trí biên độ lớn lực phục hồi đạt cực đại.

Câu 4: Tìm phát biểu sai? Trong con lắc lò xo, ta luôn có

A. \(F_{\tilde{n}h}^{\min }=k\left( \Delta {{l}_{0}}-A \right)\left( N \right)\)

B. \(\left| F_{\tilde{n}h}^{{}} \right|=k.\left| \Delta l \right|\left( N \right)\).

C. \(F_{\tilde{n}h}^{\max }=k\left( \Delta {{l}_{0}}+A \right)\left( N \right)\).

D. \({{F}_{hp}}=ma\left( N \right)\).

Câu 5: Tìm phát biểu đúng?

A. Lực kéo về chính là lực đàn hồi.

B. Lực kéo về là lực nén của lò xo.

C. Con lắc lò xo nằm ngang, lực kéo về là lực kéo.

D. Trong con lắc lò xo, lực kéo về là tổng hợp của tất cả các lực tác dụng lên vật.

Câu 6: Con lắc lò xo nằm ngang, đồ thị mô tả mối quan hệ giữa li độ của dao động và lực đàn hồi có dạng

A. Đoạn thẳng đi qua gốc tọa độ.

B. Đường tròn.

C. Đoạn thẳng không qua gốc tọa độ.

D. Đường thẳng không qua gốc tọa độ.

Câu 7: Con lắc lò xo dao động điều hòa, phát biểu nào sau đây đúng?

A. Con lắc lò xo nằm ngang, có lực đàn hồi khác lực phục hồi.

B. Độ lớn lực đàn hồi cực đại khi vật ở vị trí biên.

C. Con lắc lò xo nằm ngang, độ lớn lực đàn hồi bằng với độ lớn lực phục hồi.

D. Ở vị trí cân bằng lực đàn hồi và lực phục hồi là một.

Câu 8: Một con lắc lò xo gồm vật có khối lượng \(m=100\,\text{g}\), treo vào lò xo có độ cứng \(k=20\,\text{N/m}\). Vật dao động theo phương thẳng đứng trên quỹ đạo dài 10 cm, chọn chiều dương hướng xuống. Cho biết chiều dài ban đầu của lò xo là 40cm. Xác định chiều dài cực đại, cực tiểu của lò xo?

A. 45; 50 cm.                    

B. 50; 45 cm.                    

C. 55; 50 cm.                    

D. 50; 40cm.

Câu 9: Một con lắc lò xo gồm vật có khối lượng \(m=100\,\text{g}\), treo vào lò xo có độ cứng \(k=20\,\text{N/m}\). Vật dao động theo phương thẳng đứng trên quỹ đạo dài 10 cm, chọn chiều dương hướng xuống. Cho biết chiều dài ban đầu của lò xo là 40cm. Hãy xác định độ lớn lực đàn hồi cực đại, cực tiểu của lò xo?

A. 2; 1 N.                          

B. 2; 0N.                           

C. 3; 2N.                           

D. 4; 2N.

Câu 10: Một con lắc lò xo treo thẳng đứng gồm một vật \(m=1000\,\text{g}\), lò xo có độ cứng \(k=100\,\text{N/m}\). Kéo vật ra khỏi vị trí cân bằng \(x=+2\,\text{cm}\) và truyền vận tốc \(v=+20\sqrt{3}\text{ cm/s}\) theo phương lò xo. Cho \(g={{\pi }^{2}}=10\,\text{m/}{{\text{s}}^{\text{2}}}\), lực đàn hồi cực đại và cực tiểu của lò xo có độ lớn là bao nhiêu?

A. 1,4N; 0,6N.                  

B. 14N; 6N.                      

C. 14 N; 0N.                     

D. không đáp án.

---(Nội dung đầy đủ, chi tiết từ câu 11 đến câu 30 của tài liệu các em vui lòng xem Online hoặc Đăng nhập vào HOC247 đề tải về máy)---

ĐÁP ÁN

1-D	2-D	3-D	4-A	5-D	6-A	7-C	8-D	9-B	10-B
11-A	12-D	13-B	14-A	15-C	16-A	17-B	18-C	19-D	20-A
21-D	22-B	23-D	24-B	25-A	26-A	27-A	28-C	29-D	30-A

Trên đây là một phần trích đoạn nội dung Phương pháp giải bài toán lực đàn hồi, lực hồi phục môn Vật Lý 12 năm 2021-2022. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.