Các điểm dao động cực đại, cực tiểu đồng thời cùng pha, ngược pha với nguồn trên AB môn Vật Lý 12

1.1. Cách 1

Nguồn 2: \({{u}_{A}}={{u}_{B}}=a\cos \left( \omega t \right)\Rightarrow \left\{ \begin{align} & {{u}_{AM}}=a\cos \left( \omega t-\frac{2\pi AM}{\lambda } \right) \\ & {{u}_{BM}}=a\cos \left( \omega t-\frac{2\pi BM}{\lambda } \right) \\ \end{align} \right.\)

Do đó \ ({{u} _ {M}} = {{u} _ {AM}} + {{u} _ {BM}} = 2a \ cos \ left (\ omega t- \ frac {\ pi. AB} {\ lambda} \ right) \ cos \ frac {\ pi \ left (MA-MB \ right)} {\ lambda} \).

Để tồn tại cực đại, đồng thời cực tiểu, cùng pha, ngược pha với nguồn thì \ (AB = n \ lambda \).

Khi đó: \ ({{u} _ {M}} = 2a \ cos \ left (\ omega tn \ pi \ right) \ cos \ frac {\ pi \ left (MA-MB \ right)} {\ lambda} \).

If n chẵn, cực đại cùng pha với nguồn khi \ (MA-MB = 2k \ lambda \).

If n lẻ, cực đại cùng pha với nguồn khi: \ (MA-MB = \ left (2k + 1 \ right) \ lambda \).

1.2. Cách 2: Vẽ hình và đếm

một. Cực đại cùng pha (ngược pha) với nguồn.

Để tồn tại cực đại, đồng thời cực tiểu, cùng pha, ngược pha với nguồn thì \ (AB = n \ lambda \).

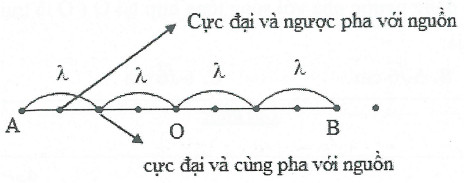
b. Cực đại cùng pha (ngược pha) với trung điểm của AB.

+) Các điểm dao động cùng pha cách nhau \ (k \ lambda. \).

+) Các điểm dao động ngược pha nhau \ (\ left (k + 0,5 \ right) \ lambda \).

+) Các điểm cực đại cách nhau \ (d = \ frac {\ lambda} {2} \), các điểm cực tiểu cách nhau \ (d = \ frac {\ lambda} {2} \).

Xét điểm M trên trung trực của \({{S}_{1}},{{S}_{2}}:{{S}_{1}}M={{S}_{2}}M=d\left( d\ge 4,8\lambda  \right)\).

Khi đó: \({{u}_{1M}}=a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)\) và \){{u}_{2M}}=a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)\).

Phương trình tại M là \({{u}_{M}}=2a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)\).

\(d\ge 4,8\lambda \Rightarrow k\ge 4,8\Rightarrow {{k}_{\min }}=5\).

Do đó \({{d}_{\min }}=5\lambda \Rightarrow {{d}_{\left( M;{{S}_{1}}{{S}_{2}} \right)}}=\sqrt{{{\left( 5\lambda  \right)}^{2}}-{{\left( 4,8\lambda  \right)}^{2}}}=1,4\lambda \).

Chọn D.

Ví dụ 2: Hai nguồn phát sóng kết hợp \({{S}_{1}},{{S}_{2}}\) trên mặt nước cách nhau 20cm phát ra hai dao động điều hòa cùng phương, cùng tần số \(f=40\,Hz\) và pha ban đầu bằng không. Biết tốc độ truyền sóng trên mặt chất lỏng \(v=3,2m/s\).  Những điểm nằm trên đường trung trực của đoạn \({{S}_{1}}{{S}_{2}}\) mà sóng tổng hợp tại đó luôn dao động ngược pha với sóng tổng hợp tại O (O là trung điểm của \({{S}_{1}}{{S}_{2}}\)) cách o một khoảng nhỏ nhất là:

A. \(4\sqrt{6}\,cm\)           

B. \(5\sqrt{6}\,cm\)                

C. \(6\sqrt{6}\,cm\)           

D. \(14\,cm\) .

Lời giải

Ta có: \(\lambda =\frac{v}{f}=8\,cm\).

Giả sử hai sóng tại \({{S}_{1}},{{S}_{2}}\) có dạng: \){{u}_{1}}={{u}_{2}}=a\cos \left( \omega t \right)\).

Phương trình dao động tại M: \({{u}_{M}}=2a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)\).

(với d là khoảng cách từ M đến \({{S}_{1}},{{S}_{2}}\))

 Phương trình dao động tại O: \({{u}_{O}}=2a\cos \left( \omega t-\frac{2\pi O{{S}_{1}}}{\lambda } \right)\)

Theo bài ra ta có M và O dao động ngược pha nên: \(\frac{2\pi }{\lambda }\left( d-OA \right)=\left( 2k+1 \right)\pi \)

\(\Rightarrow d-O{{S}_{1}}=\left( k+0,5 \right)\lambda \). Do đó \({{d}_{\min }}=O{{S}_{1}}+0,5\lambda =10+0,5.8=14\,cm\)

Suy ra: \(O{{M}_{\min }}=\sqrt{{{14}^{2}}-{{10}^{2}}}=4\sqrt{6}\,cm\).

Chọn A.

Ví dụ 3: Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình \({{u}_{A}}={{u}_{B}}=a\cos 50\pi t\) (với t tính bằng s). Tốc độ truyền sóng ở mặt chất lỏng là \(v=2m/s\). Gọi O là trung điểm của AB, điểm M ở chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phân tử chất lỏng tại M dao động ngược pha với phần tử tại O. Khoảng cách MO là:

A. 14,42 cm                      

B. 9,38 cm                             

C. 5,00 cm            

D. 7,93 cm

Lời giải

Ta có: \(f=\frac{\omega }{2\pi }=25\,Hz\,.\,\lambda =\frac{v}{f}=8\,cm\)Bước sóng:

Phương trình sóng tại điểm M và O lần lượt là:

\({{u}_{M}}=2a\cos \left( 50\pi t-\frac{2\pi d}{\lambda } \right),{{u}_{O}}=2a\cos \left( 50\pi t-\frac{2\pi OA}{\lambda } \right)\).

Theo bài ra ta có M và O dao động ngược pha nên: \(\frac{2\pi }{\lambda }\left( d-OA \right)=\left( 2k+1 \right)\pi \)

\(\Rightarrow d-OA=\left( k+0,5 \right)\lambda \). Do đó \({{d}_{\min }}=OA+0,5\lambda =9+0,5.8=13\,cm\).

Suy ra: \(O{{M}_{\min }}=\sqrt{{{13}^{2}}-{{9}^{2}}}=9,38\)cm.

Chọn B.

Ví dụ 4: Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp \({{S}_{1}}\) và \({{S}_{2}}\)cách nhau 30 cm, dao động theo phương thẳng đứng với phương trình \(u=4\cos 100\pi t\,\left( mm \right)\). Biết tốc độ truyền sóng trên mặt chất lỏng là \(1,5m/s\). Phần tử O thuộc bề mặt chất lỏng là trung điểm \({{S}_{1}}{{S}_{2}}\). Điểm trên mặt chất lỏng thuộc trung trực của \({{S}_{1}}{{S}_{2}}\) dao động cùng pha với O, gần O nhất, cách O đoạn:

A. 11,7 cm                         B. 9,9 cm                                C. 19 cm                            D. 18 cm

Lời giải

Ta có: \(f=\frac{\omega }{2\pi }=50Hz.\)

Bước sóng: \(\lambda =\frac{v}{f}=3\,cm\)

Phương trình sóng tại điểm M và O lần lượt là:

\({{u}_{M}}=2a\cos \left( 100\pi t-\frac{2\pi d}{\lambda } \right),{{u}_{O}}=2a\cos \left( 100\pi t-\frac{2\pi OA}{\lambda } \right)\).

Theo bài ra ta có: M và O dao động cùng pha nên \(d-O{{S}_{1}}=k\lambda \)

\({{d}_{\min }}=O{{S}_{1}}+\lambda =18\Rightarrow M{{O}_{\min }}=\sqrt{{{18}^{2}}-{{15}^{2}}}=9,9\,cm\).

Chọn B.

Ví dụ 5: Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 16 cm dao động theo phương trình \(u=a\cos \left( \omega t \right)\) trên mặt nước, coi biên độ không đổi, bước sóng \(\lambda =2,5\,cm\). Gọi O là trung điểm của AB.  Một điểm nằm trên đường trung trực AB, dao động cùng pha với các nguồn A và B, cách A hoặc B một đoạn nhỏ nhất là:

A. 12 cm                            B. 10 cm                                 C. 13,5 cm                         D. 13 cm

Lời giải

Phương trình sóng của 2 nguồn là:

\({{u}_{A}}={{u}_{B}}=a\cos \left( \omega t \right)\).

Phương trình sóng tại điểm M là:

\({{u}_{M}}=2a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)\).

Điểm M dao động cùng pha với nguồn khi \(d=k\lambda =2,5k\ge \frac{AB}{2}=8\Rightarrow k\ge 3,2\Rightarrow {{k}_{\min }}=4\). Khi đó \({{d}_{\min }}=10\,cm\).

Chọn B.

Ví dụ 6: Trên mặt nước có hai nguồn kết hợp A, B cách nhau 16 cm dao động theo phương trình \({{u}_{A}}={{u}_{B}}=a\cos \left( 30\pi t \right)\,mm\). Tốc độ truyền sóng trên mặt nước là \(1,2m/s\) và biên độ sóng không đổi trong quá trình truyền. Điểm gần nhất ngược pha với các nguồn nằm trên đường trung trực của AB cách AB một đoạn:

A. 6 cm                              B. 4 cm                                   C. \(4\sqrt{5}\) cm            D. 12 cm

Lời giải

Ta có: \(f=15\,Hz,\lambda =\frac{v}{f}=8cm.\)

Phương trình sóng của 2 nguồn là:

\({{u}_{A}}={{u}_{B}}=a\cos \left( 30\pi t \right)\).

Phương trình sóng tại điểm M là:

\({{u}_{M}}=2a\cos \left( 30\pi t-\frac{2\pi d}{\lambda } \right)\).

Điểm M dao động ngược pha với nguồn khi

\(d=\left( k+0,5 \right)\lambda =8\left( k+0,5 \right)\ge \frac{AB}{2}=8\Rightarrow k\ge 0,5\Rightarrow {{k}_{\min }}=1.\) Khi đó \){{d}_{\min }}=12\,cm\).

Suy ra \(O{{M}_{\min }}=\sqrt{d_{\min }^{2}-{{\left( \frac{AB}{2} \right)}^{2}}}=4\sqrt{5}\,cm\).

Chọn C.

Ví dụ 7: Trong một thí nghiệm giao thoa sóng nước, hai nguồn \({{S}_{1}}\) và \({{S}_{2}}\) cách nhau 16 cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số \(80\,Hz\). Tốc độ truyền sóng trên mặt nước là \(40\,cm/s\). Ở mặt nước, gọi d là đường trung trực của đoạn \({{S}_{1}}{{S}_{2}}\). Trên d, điểm M ở cách \({{S}_{1}}\) 10 cm; điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây?

A. 6,8 mm                          B. 8,8 mm                               C. 9,8 mm                          D. 7,8 mm

Lời giải

Ta có: \(\lambda =\frac{v}{f}=\frac{40}{80}=0,5\,cm\)

Phương trình sóng tại M và N có dạng:

\({{u}_{M}}=2a\cos \left( \omega t-\frac{2\pi {{d}_{M}}}{\lambda } \right)\).

\({{u}_{N}}=2a\cos \left( \omega t-\frac{2\pi {{d}_{N}}}{\lambda } \right)\).

Để 2 điểm M, N cùng pha thì \({{d}_{M}}-{{d}_{N}}=k\lambda \Leftrightarrow 10-{{d}_{N}}=0,5k\).

Để M, N ngắn nhất thì 

\(\begin{array}{l} \left( \begin{array}{l} k = 1\\ k = - 1 \end{array} \right. \Rightarrow \left( \begin{array}{l} {d_N} = 9,5\\ {d_N} = 10,5 \end{array} \right.\\ \left( \begin{array}{l} MN = OM - ON = \sqrt {{{10}^2} - {8^2}} - \sqrt {9,{5^2} - {8^2}} = 0,88{\mkern 1mu} cm\\ MN = ON - OM = \sqrt {10,{5^2} - {8^2}} - \sqrt {{{10}^2} - {8^2}} = 0,8{\mkern 1mu} cm \end{array} \right.. \end{array}\)

Chọn D.

Ví dụ 8: Trong một thí nghiệm giao thoa sóng nước, hai nguồn \({{S}_{1}}\) và \({{S}_{2}}\) cách nhau 14 cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số \(40\,Hz\). Tốc độ truyền sóng trên mặt nước là \(1,2m/s.\) Ở mặt nước, gọi d là đường trung trực của đoạn \({{S}_{1}}{{S}_{2}}\). Trên d, điểm M ở cách \({{S}_{1}}\)12cm; điểm N dao động ngược pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây?

A. 5,0 cm                           B. 2,0 cm                                C. 1,8 cm                           D. 0,5 cm

Lời giải

Ta có: \(\lambda =\frac{v}{f}=\frac{120}{40}=3\,cm\).

Phương trình sóng tại M và N có dạng:

\({{u}_{M}}=2a\cos \left( \omega t-\frac{2\pi {{d}_{M}}}{\lambda } \right)\)

\({{u}_{N}}=2a\cos \left( \omega t-\frac{2\pi {{d}_{N}}}{\lambda } \right)\)

Để 2 điểm M, N ngược pha thì \({{d}_{M}}-{{d}_{N}}=\left( k+0,5 \right)\lambda \Leftrightarrow 12-{{d}_{N}}=3\left( k+0,5 \right)\).

Để M, N ngắn nhất thì: \(\left( \begin{array}{l} k = 0\\ k = - 1 \end{array} \right. \Rightarrow \left( \begin{array}{l} {d_N} = 10,5\\ {d_N} = 13,5 \end{array} \right.\)

\(\left( \begin{align} & MN=OM-ON=\sqrt{{{12}^{2}}-{{7}^{2}}}-\sqrt{10,{{5}^{2}}-{{7}^{2}}}=1,92\,cm \\ & MN=ON-OM=\sqrt{13,{{5}^{2}}-{{7}^{2}}}-\sqrt{{{12}^{2}}-{{7}^{2}}}=1,79\,cm \\ \end{align} \right.\)

Chọn C.

Ví dụ 9: Hai mũi nhọn A, B cách nhau 10 cm gắn vào đầu một cần rung có tần số \(f=50\,Hz\), đặt chạm nhẹ vào mặt một chất lỏng. Tốc  độ truyền sóng trên mặt chất lỏng \(v=0,25m/s\). Hai nguồn A, B dao động theo phương thẳng đứng với cùng phương trình \({{u}_{A}}={{u}_{B}}=a\cos \left( \omega t \right)\,\left( cm \right)\). Một điểm M trên mặt chất lỏng cách đều A, B một khoảng \(d=8\,cm\). Gọi \({{N}_{1}}\) và \({{N}_{2}}\) là hai điểm gần M nhất dao động cùng pha với M. Khoảng cách giữa hai điểm \({{N}_{1}}\) và \({{N}_{2}}\) là:

A. 1,28 cm                         B. 0,63 cm                              C. 0,65 cm                         D. 0,02 cm

Lời giải

Ta có: \(\lambda =\frac{v}{f}=\frac{25}{50}=0,5\,cm\)

Phương trình sóng tại M và N có dạng:

\({{u}_{M}}=2a\cos \left( \omega t-\frac{2\pi {{d}_{M}}}{\lambda } \right)\)

\({{u}_{N}}=2a\cos \left( \omega t-\frac{2\pi {{d}_{N}}}{\lambda } \right)\)

Để 2 điểm M, N cùng pha thì \({{d}_{M}}-{{d}_{N}}=k\lambda \Leftrightarrow 8-{{d}_{N}}=0,5k\).

Để M, N ngắn nhất thì \(\left( \begin{array}{l} k = - 1\\ k = 1 \end{array} \right. \Rightarrow \left( \begin{array}{l} {d_{{N_1}}} = 8,5\\ {d_{{N_1}}} = 7,5 \end{array} \right.\)

\({{N}_{1}}{{N}_{2}}=O{{N}_{1}}-O{{N}_{2}}=\sqrt{d_{{{N}_{1}}}^{2}-{{5}^{2}}}-\sqrt{d_{{{N}_{2}}}^{2}-{{5}^{2}}}=1,28\,cm\). Chọn A.

Ví dụ 10: Trên mặt nước có 2 nguồn sóng giống hệt nhau A và B cách nhau một khoảng \(AB=48\,cm\). Bước sóng \(\lambda =1,8\,cm\). Hai điểm M và N trên mặt nước cùng cách đều trung điểm của đoạn AB một đoạn 10 cm và cùng cách đều 2 nguồn sóng và A và B. Số điểm trên đoạn MN dao động cùng pha với 2 nguồn là:

A. 2                                    B. 18                                       C. 4                                    D. 9

Lời giải

Phương trình sóng tại điểm I trên trung trực là:

\({{u}_{1}}=2a\cos \left( \omega t-\frac{2\pi }{\lambda } \right)\) (với \({{d}_{1}}={{d}_{2}}=d=IA\))

Điểm cùng pha với 2 nguồn thỏa mãn \(d=k\lambda .\) Gọi O là trung điểm của AB.

Số điểm dao động cùng pha với nguồn trên đoạn OM thỏa mãn \(24\le k\lambda \le \sqrt{{{10}^{2}}+{{24}^{2}}}\).

\(\Leftrightarrow 13,33\le k\le 14,44\Leftrightarrow k=14\)

Do đó trên MN có tổng cộng 2 điểm dao động cùng pha với 2 nguồn. Chọn A

Câu 1: Trên mặt nước tại hai điểm A, B có hai nguồn sóng kết hợp dao động cùng pha, lan truyền với bước sóng \(\lambda \). Biết \(AB=11\lambda \). Xác định số điểm dao động với biên độ cực đại và ngược pha với hai nguồn trên đoạn Ab (không tính hai điểm A, B):

A. 12                                  B. 23                                  C. 11                                  D. 21

Câu 2: Hai mũi nhọn A, B cách nhau 8 cm gắn vào đầu một cần rung có tần số \(f=100\,Hz\), đặt chạm nhẹ vào mặt một chất lỏng. Tốc độ truyền sóng trên mặt chất lỏng \(v=0,8\,m/s\). Hai nguồn A, B dao động theo phương thẳng đứng với cùng phương trình \({{u}_{A}}={{u}_{B}}=a\cos \left( \omega t \right)\,cm\). Một điểm M trên mặt chất lỏng cách đều A, B một khoảng \(d=8\,cm\). Tìm trên đường trung trực của AB một điểm \({{M}_{1}}\) gần M nhất và dao động cùng pha với M.

A. \)M{{M}_{2}}=0,2\,cm;\,M{{M}_{1}}=0,4\,cm\)                

B. \)M{{M}_{2}}=0,91\,cm;\,M{{M}_{1}}=0,94\,cm\)

C. \)M{{M}_{2}}=9,1\,cm;\,M{{M}_{1}}=9,4\,cm\)                 

D. \)M{{M}_{2}}=2\,cm;\,M{{M}_{1}}=4\,cm\)

Câu 3: Trên mặt nước có hai nguồn sóng giống hệt nhau A và B cách nhau một khoảng \(AB=24\,cm\). Bước sóng \(\lambda =2,5\,cm\). Hai điểm M và N trên mặt nước cùng cách đều trung điểm của đoạn AB một đoạn 16 cm và cùng cách đều 2 nguồn sóng A và B. Số điểm trên đoạn MN dao động cùng pha với 2 nguồn là:

A. 7                                    B. 8                                    C. 6                                    D. 9

Câu 4: Trên mặt nước có hai nguồn kết hợp \({{S}_{1}},{{S}_{2}}\) cách nhau \(6\sqrt{2}\,cm\) dao động có phương trình \(u=a\cos \left( 20\pi t \right)\,mm\). Tốc độ truyền sóng trên mặt nước là \(0,4\,m/s\) và biên độ sóng không đổi trong quá trình truyền. Điểm gần nhất ngược pha với các nguồn nằm trên đường trung trực của \({{S}_{1}}{{S}_{2}}\) cách \({{S}_{1}}{{S}_{2}}\) một đoạn:

A. 6 cm                              B. 2 cm                              C. \(3\sqrt{2}\,cm\)          D. 18 cm

Câu 5: Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp \({{S}_{1}}\) và \({{S}_{2}}\) cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình \(u=2\cos 40\pi t\,\left( mm \right)\). Biết tốc độ truyền sóng trên mặt chất lỏng là \(40\,cm/s\). Phần tử O thuộc bề mặt chất lỏng là trung điểm của \({{S}_{1}}{{S}_{2}}\). Điểm trên mặt chất lỏng thuộc trung trực của \({{S}_{1}}{{S}_{2}}\) dao động cùng pha với O, gần O nhất, cách O đoạn bằng:

A. 6,6 cm                           B. 8,2 cm                           C. 12 cm                            D. 16cm

Câu 6: Trong hiện tượng giao thoa sóng nước, hai nguồn sóng tại A và B cách nhau 10 cm dao động cùng pha, cùng tần số \(f=40\,Hz\). Gọi H là trung điểm đoạn AB, M là điểm trên đường trung trực của AB và dao động cùng pha với hai nguồn. Tốc độ truyền sóng trên mặt nước là \(80\,cm/s\). Khoảng cách gần nhất từ M đến H là:

A. 6, 24 cm                        B. 3,32 cm                         C. 2,45 cm                         D. 4,25 cm

Câu 7: Trên mặt chất lỏng có hai nguồn sóng kết hợp phát ra hai dao động \({{u}_{1}}=a\cos \omega t;\) \({{u}_{2}}=a\sin \omega t\). Khoảng cách giữa hai nguồn là \({{S}_{1}}{{S}_{2}}=3,25\lambda \). Hỏi trên đoạn \({{S}_{1}}{{S}_{2}}\) có mấy điểm cực đại dao động cùng pha với \({{u}_{2}}\).

A. 3 điểm                           B. 4 điểm                           C. 5 điểm                           D. 6 điểm

Câu 8: Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn \({{S}_{1}}{{S}_{2}}=9\lambda \) phát ra dao động \(u=\cos \left( \omega t \right)\). Trên đoạn \({{S}_{1}}{{S}_{2}}\), số điểm có biên độ cực đại cùng pha với nhau và ngược pha với nguồn (không kể hai nguồn) là:

A. 8                                    B. 9                                    C. 17                                  D. 16

Câu 9: Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6 cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoảng 8cm. Hỏi trên đoạn CO, số điểm dao động cùng pha với nguồn là:

A. 2                                    B. 3                                    C. 4                                    D. 5

Câu 10: Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6 cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoảng 8cm. Hỏi trên đoạn CO, số điểm dao động ngược pha với nguồn là:

A. 2                                    B. 3                                    C. 4                                    D. 5

---Để xem đầy đủ nội dung từ câu 11 đến câu 15, vui lòng đăng nhập vào trang hoc247.net để xem online hoặc tải về máy tính---

Trên đây là trích dẫn một phần nội dung tài liệu Các điểm dao động cực đại, cực tiểu đồng thời cùng pha, ngược pha với nguồn trên AB môn Vật lý 12 năm 2021-2022. Để xem thêm nhiều tư tưởng khác nhau, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học tập tốt và đạt được thành tích cao trong học tập.