Mời quý thầy cô cùng các em học sinh cùng tham khảo Đề thi giữa HK2 môn Toán 12 năm 2022-2023 trường THPT Trần Phú có đáp án được Học247 biên tập và tổng hợp dưới đây. Hãy truy cập ngay hoc247.net để thử sức với những đề thi hot nhất nhé!
|
SỞ GD & ĐT TRƯỜNG THPT TRẦN PHÚ
(Đề gồm 06 trang ) |
KÌ THI GIỮA HỌC KÌ 2 NĂM 2022 - 2023 MÔN : TOÁN LỚP 12 Thời gian làm bài: 90 phút. (50 câu trắc nghiệm) |
Đề bài
Họ và tên học sinh:…………………………………... Mã số học sinh:………………………….
PHẦN TRẮC NGHIỆM
Câu 1: Họ tất cả các nguyên hàm của hàm số \(y={{x}^{3}}\) là (NB)
|
A. \(\frac{{{x}^{4}}}{4}+C.\) |
B. \(3{{x}^{2}}+C.\) |
C. \({{x}^{4}}+C.\) |
D. \({{x}^{2}}+C.\) |
Câu 2: Họ tất cả các nguyên hàm của hàm số \(y=\frac{1}{{{\sin }^{2}}x}\) là (NB)
|
A. \(-\cot x+C.\) |
B. \(\cot x+C.\) |
C. \(-\tan x+C.\) |
D. \(\tan x+C.\) |
Câu 3: Họ tất cả các nguyên hàm của hàm số \(y={{a}^{x}}\left( a>0,a\ne 1 \right)\) là (NB)
|
A. \(\frac{{{a}^{x}}}{\ln a}+C.\) |
B. \({{a}^{x}}+C.\) |
C. \({{a}^{x}}.\ln a+C.\) |
D. \({{e}^{x}}+C.\) |
Câu 4: Xét \(f\left( x \right)\) là một hàm số tuỳ ý, \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên khoảng \(K.\) Hàm số nào dưới đây là một nguyên hàm của \(f\left( x \right)\) ?(NB)
|
A. \(F\left( x \right)+2021.\) |
B. \(F\left( x \right)+2021x.\) |
C. \(2021F\left( x \right).\) |
D. \(\frac{F\left( x \right)}{2021}.\) |
Câu 5: Xét hàm số \(f\left( x \right)\) tuỳ ý, liên tục trên khoảng \(K.\) Với mọi số thực \(k\ne 0,\) mệnh đề nào sau đây đúng ? (NB)
|
A. \(\int{kf\left( x \right)}\text{d}x=k\int{f\left( x \right)}\text{d}x.\) |
B. \(\int{kf\left( x \right)}\text{d}x=\frac{1}{k}\int{f\left( x \right)}\text{d}x.\) |
|
C. \(\int{kf\left( x \right)}\text{d}x=kf\left( x \right).\) |
D. \(\int{kf\left( x \right)}\text{d}x=k+\int{f\left( x \right)}\text{d}x.\) |
Câu 6: Xét các hàm số \(f\left( x \right),g\left( x \right)\) tuỳ ý, liên tục trên khoảng \(K.\) Mệnh đề nào dưới đây đúng ? (NB)
|
A. \(\int{\left[ f\left( x \right)-g\left( x \right) \right]}\text{d}x=\int{f\left( x \right)}\text{d}x-\int{g\left( x \right)}\text{d}x.\) |
|
B. \(\int{\left[ f\left( x \right)-g\left( x \right) \right]}\text{d}x=\int{f\left( x \right)}\text{d}x+\int{g\left( x \right)}\text{d}x.\) |
|
C. \(\int{\left[ f\left( x \right)-g\left( x \right) \right]}\text{d}x=\int{g\left( x \right)}\text{d}x-\int{f\left( x \right)}\text{d}x.\) |
|
D. \(\int{\left[ f\left( x \right)-g\left( x \right) \right]}\text{d}x=\int{f\left( x \right)}\text{d}x.\int{g\left( x \right)}\text{d}x.\) |
Câu 7: Xét hai hàm số \(u=u\left( x \right)\) và \(v=v\left( x \right)\) có đạo hàm liên tục trên \(K\). Khi đó \(\int{u\text{d}v}\) bằng (NB)
|
A. \(uv-\int{v\text{d}u}.\) |
B. \(uv-\int{u\text{d}v}.\) |
C. \(uv+\int{v\text{d}u}.\) |
D. \(uv+\int{u\text{d}v}.\) |
Câu 8: Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ a;b \right]\). Khi đó \(\int\limits_{a}^{b}{{f}'\left( x \right)\text{d}x}\) bằng (NB)
|
A. \(\text{f}\left( b \right)-f\left( a \right).\) |
B. \(\text{f}\left( b \right)+f\left( a \right).\) |
C. \(\text{f}\left( a \right)-f\left( b \right).\) |
D. \(b-a.\) |
Câu 9: Xét hàm số \(f\left( x \right)\) tuỳ ý, liên tục trên đoạn \(\left[ 1;3 \right],\) \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right).\) Mệnh đề nào dưới đây đúng ? (NB)
|
A. \(\int\limits_{1}^{3}{f\left( x \right)\text{d}x}=F\left( 3 \right)-F\left( 1 \right).\) |
B. \(\int\limits_{1}^{3}{f\left( x \right)\text{d}x}=F\left( 1 \right)-F\left( 3 \right).\) |
|
C. \(\int\limits_{1}^{3}{f\left( x \right)\text{d}x}=F\left( 3 \right)+F\left( 1 \right).\) |
D. \(\int\limits_{1}^{3}{f\left( x \right)\text{d}x}=\int\limits_{3}^{1}{f\left( x \right)\text{d}x}.\) |
Câu 10: Cho hàm số \(f\left( x \right)\) liên tục và không âm trên đoạn \(\left[ a;b \right],\) \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right).\) Diện tích hình thang cong giới hạn bởi các đường thẳng \(x=a,\text{ }x=b\text{ }\left( a < b \right),\) trục hoành và đồ thị hàm số \(f\left( x \right)\) được tính theo công thức nào dưới đây ? (NB)
|
A. \(F\left( b \right)-F\left( a \right).\) |
B. \(F\left( b \right)+F\left( a \right).\) |
C. \(F\left( a \right)-F\left( b \right).\) |
D. \(\pi \left[ F\left( b \right)+F\left( a \right) \right].\). |
Câu 11: Biết \(\int\limits_{-1}^{3}{f\left( x \right)\text{d}x}=3\) và \(\int\limits_{3}^{4}{f\left( x \right)\text{d}x}=-1.\) Khi đó \(\int\limits_{-1}^{4}{f\left( x \right)\text{d}x}\) bằng (NB)
|
A. \(2.\) |
B. \(4.\) |
C. \(-3.\) |
D. \(3.\) |
Câu 12: Biết \(\int\limits_{1}^{5}{f\left( x \right)\text{d}x}=4\) và \(\int\limits_{1}^{5}{g\left( x \right)\text{d}x}=1.\) Khi đó \(\int\limits_{1}^{5}{\left[ f\left( x \right)+g\left( x \right) \right]\text{d}x}\) bằng (NB)
|
A. \(5.\) |
B. \(3.\) |
C. \(4.\) |
D. \(2.\) |
Câu 13: Biết \(\int\limits_{2}^{3}{f\left( x \right)\text{d}x}=6.\) Khi đó \(\int\limits_{2}^{3}{\frac{1}{2}f\left( x \right)\text{d}x}\) bằng (NB)
|
A. \(3.\) |
B. \(\frac{13}{2}.\) |
C. \(\sqrt{6}.\) |
D. \(4.\) |
Câu 14: Biết \(\int\limits_{1}^{2}{f\left( x \right)\text{d}x}=2.\) Khi đó \(\int\limits_{2}^{1}{f\left( x \right)\text{d}x}\) bằng (NB)
|
A. \(-2.\) |
B. \(2.\) |
C. \(\frac{1}{2}.\) |
D. \(-\frac{1}{2}.\) |
Câu 15 : Trong không gian \(Oxyz,\) cho vectơ \(\overrightarrow{a}=3\overrightarrow{i}-4\overrightarrow{k}.\) Tọa độ của \(\overrightarrow{a}\) là (NB)
|
A. \(\left( 3;0;-4 \right).\) |
B. \(\left( 3;-4;0 \right).\) |
C. \(\left( 0;3;4 \right).\) |
D. \(\left( 0;3;-4 \right).\) |
|||||
|
Câu 16 : Trong không gian \(Oxyz,\)cho hai vectơ \(\overrightarrow{a}=\left( {{a}_{1}};{{a}_{2}};{{a}_{3}} \right)\)và \(\overrightarrow{b}=\left( {{b}_{1}};{{b}_{2}};{{b}_{3}} \right).\) Khẳng định nào dưới đây là sai ? (NB)
|
|
|||||||
Câu 17: Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right)\) có phương trình: \({{x}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=4\). Tọa độ tâm \(I\) và bán kính \(R\) của \(\left( S \right)\) là (NB)
|
A.\(I\left( 0;1;3 \right),\,\,R=2.\) |
B. \(I\left( 0;-1;-3 \right),\,\,R=2.\) |
|
C. \(I\left( 0;1;3 \right),\,\,R=4.\) |
D. \(I\left( 0;-1;-3 \right),\,\,R=4.\) |
Câu 18 : Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right)\) có phương trình: \(x-2y+3z-1=0\). Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)\) ? (NB)
|
A. \(\left( 1;-2;3 \right).\) |
B. \(\left( 1;-2;1 \right).\) |
C. \(\left( -2;3;-1 \right).\) |
D. \(\left( 1;2;3 \right).\) |
Câu 19: Trong không gian \(Oxyz,\) cho hai mặt phẳng \(\left( P \right):\,x-2y+3z-1=0\) và \(\left( Q \right):-x+2y-3z+2=0.\) Mệnh đề nào dưới đây đung ?(NB)
|
A. \(\left( P \right)\) cắt \(\left( Q \right).\) |
B.\(\left( P \right)\) vuông góc với \(\left( Q \right).\) |
|
C. \(\left( P \right)\) song song với \(\left( Q \right).\) |
D. \(\left( P \right)\) trùng với \(\left( Q \right).\) |
Câu 20: Trong không gian \(Oxyz,\) điểm nào sau đây thuộc mặt phẳng \(\left( \alpha \right):x-y+2z+3=0\) ?(NB)
|
A. \(M\left( 1;-1;2 \right).\) |
B. \(N\left( 4;1;0 \right).\) |
C. \(P\left( 1;4;0 \right).\) |
D. \(Q\left( 0;0;-3 \right).\) |
---(Để xem đầy đủ nội dung của phần trắc nghiệm, vui lòng xem online hoặc đăng nhập vào Học247 để tải về máy)---
PHẦN TỰ LUẬN
Câu 1: Tính tích phân \(\int\limits_{1}^{e}{\frac{\ln x}{x\sqrt{1+3\ln x}}}\text{d}x.\) (VD)
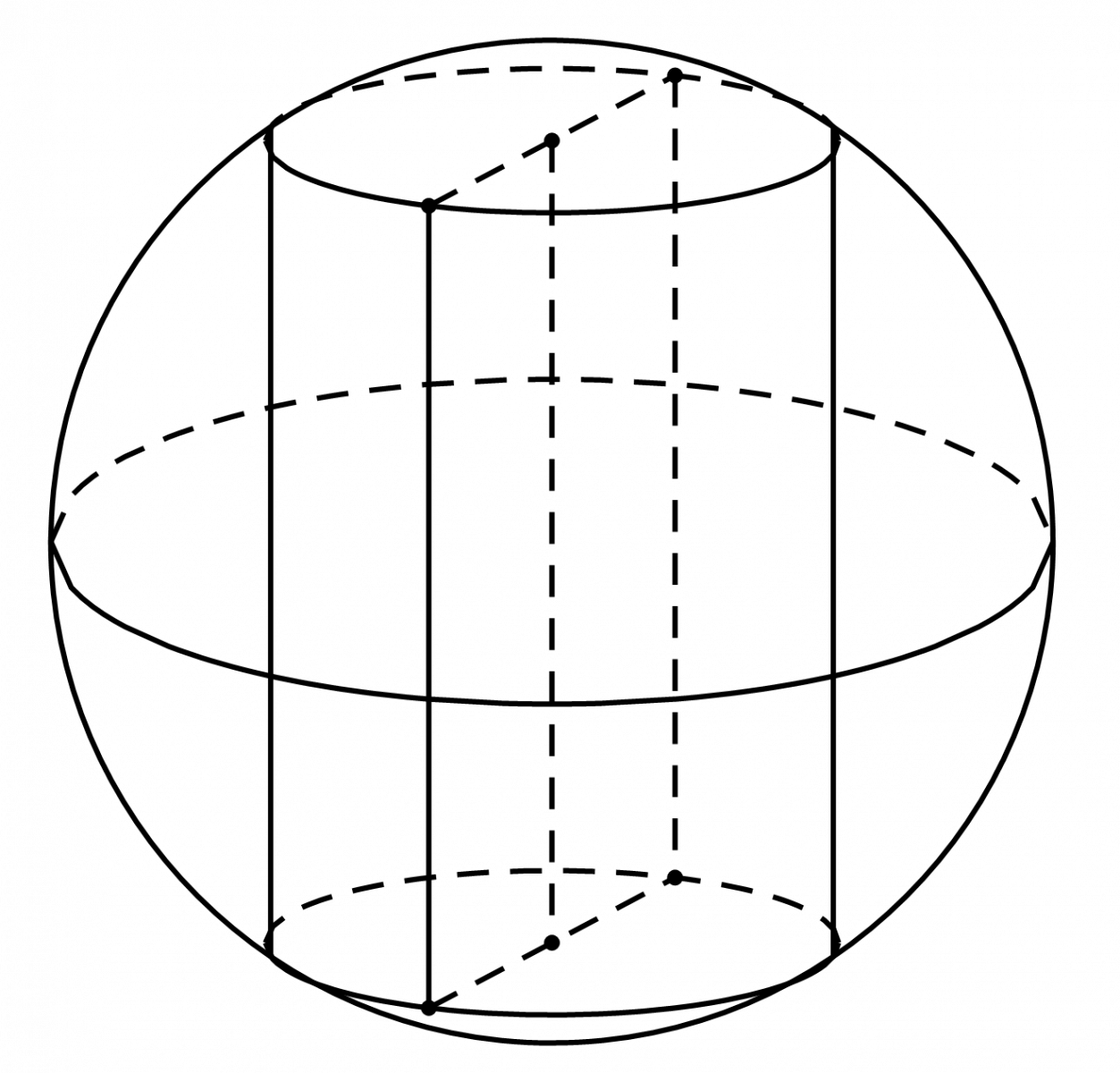
Câu 2: Một hình trụ có chiều cao bằng \(6\) nội tiếp trong một hình cầu có bán kính bằng \(5\) như hình vẽ. Tính thể tích của khối trụ đã cho. (VD)
Câu 3:
a) Cho hàm số \(y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\left( a,b,c,d\in \mathbb{R},a\ne 0 \right)\) và có đồ thị \(\left( C \right).\) Biết rằng \(\left( C \right)\) đi qua gốc tọa độ và có đồ thị hàm số \(y={f}'\left( x \right)\) cho bởi hình vẽ sau đây. Tính giá trị của \(H=f\left( 4 \right)-f\left( 2 \right)\) (VDC)
b) Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\left[ 0;1 \right]\) và \(f\left( 0 \right)+f\left( 1 \right)=0.\) Biết \(\int\limits_{0}^{1}{{{f}^{2}}\left( x \right)\text{d}x}=\frac{1}{2};\int\limits_{0}^{1}{{{f}'}}(x)\cos \pi x\text{d}x=\frac{\pi }{2}.\) Tính \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x}\) (VDC)
Đáp án và hướng dẫn giải
PHẦN TRẮC NGHIỆM( 7,0 điểm)
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Đáp án |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
|
Câu |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
Đáp án |
A |
C |
A |
A |
C |
C |
A |
A |
A |
A |
A |
A |
A |
A |
|
Câu |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
|
|
|
|
|
|
|
Đáp án |
A |
A |
A |
A |
B |
A |
B |
|
|
|
|
|
|
|
PHẦN TỰ LUẬN ( 3,0 điểm)
|
Câu hỏi |
Nội dung |
Điểm |
|
Câu 1 (1,0 điểm) |
Ta có: \(u=\sqrt{1+3\ln x}\Rightarrow {{u}^{2}}=1+3\ln x\Rightarrow \ln x=\frac{{{u}^{2}}-1}{3}.\) Đổi cận: \(\left\{ \begin{array}{l} x = 1 \Rightarrow u = 1\\ x = e \Rightarrow u = 2 \end{array} \right..\) |
0,25 |
---(Để xem đầy đủ nội dung của phần hướng dẫn giải, vui lòng xem online hoặc đăng nhập vào Học247 để tải về máy)---
Trên đây là một phần trích dẫn nội dung Đề thi giữa HK2 môn Toán 12 năm 2022-2023 trường THPT Trần Phú có đáp án. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang Hoc247.net để tải tài liệu về máy tính.
Các em quan tâm có thể tham khảo tài liệu cùng chuyên mục:
- Đề thi giữa HK2 môn Toán 12 năm 2022-2023 Trường THPT Lê Quý Đôn có đáp án
- Đề thi giữa HK2 môn Toán 12 năm 2022-2023 Trường THPT Lý Tự Trọng có đáp án
- Bộ 5 đề thi giữa HK2 môn Toán 12 năm 2021-2022 có đáp án Trường THPT Nguyễn Trãi
Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.













