Nhß║▒m gi├║p c├Īc em hß╗Źc sinh c├│ th├¬m t├Āi liß╗ću hß╗Źc tß║Łp, r├©n luyß╗ćn chuß║®n bß╗ŗ cho k├¼ thi giß╗»a HK2 m├┤n To├Īn 10 sß║»p tß╗øi, Hß╗īC247 ─æ├Ż bi├¬n soß║Īn, tß╗Ģng hß╗Żp nß╗Öi dung t├Āi liß╗ću ─Éß╗ü thi giß╗»a HK2 m├┤n To├Īn 10 CTST n─ām 2022-2023 TrŲ░ß╗Øng THPT Trß║¦n HŲ░ng ─Éß║Īo c├│ ─æ├Īp ├Īn gi├║p c├Īc em hß╗Źc tß║Łp r├©n luyß╗ćn tß╗æt hŲĪn. Hi vß╗Źng ─æß╗ü thi dŲ░ß╗øi ─æ├óy l├Ā t├Āi liß╗ću hß╗»u ├Łch cho c├Īc em trong qu├Ī tr├¼nh hß╗Źc tß║Łp v├Ā ├┤n thi. Ch├║c c├Īc em thi tß╗æt!
|
PH├ÆNG GD&─ÉT TRŲ»ß╗£NG THPT TRß║”N HŲ»NG ─Éß║ĀO |
─Éß╗Ć KIß╗éM TRA GIß╗«A Hß╗īC K├ī 2 Lß╗ÜP 10 |
I. Trß║»c nghiß╗ćm
C├óu 1. ─Éiß╗üu kiß╗ćn ─æß╗ā tam thß╗®c bß║Łc hai \(a{{x}^{2}}+bx+c\left( a\ne 0 \right)\) nhß║Łn gi├Ī trß╗ŗ dŲ░ŲĪng vß╗øi mß╗Źi \(x\in \mathbb{R}\) l├Ā:
A. \(\text{ }\!\!\Delta\!\!\text{ }>0\).
B. \(\text{ }\!\!\Delta\!\!\text{ }<0\).
C. \(\text{ }\!\!\Delta\!\!\text{ }<0\) v├Ā \(a>0\).
D. \(\text{ }\!\!\Delta\!\!\text{ }<0\) v├Ā \(a<0\).
C├óu 2. Cho ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=f\left( x \right)\) nhŲ░ h├¼nh b├¬n. Tß║Łp hß╗Żp c├Īc gi├Ī trß╗ŗ cß╗¦a \(x\) ─æß╗ā h├Ām sß╗æ \(f\left( x \right)\) nhß║Łn gi├Ī trß╗ŗ ├óm l├Ā
.jpg?enablejsapi=1)
A. \(\left( -\infty ;1 \right)\cup \left( 4;+\infty \right)\).
B. \(\left( 1;4 \right)\).
C. \(\left( -\infty ;1\left] \cup \right[4;+\infty \right)\).
D. \(\left[ 1;4 \right]\).
C├óu 3. Cho tam thß╗®c bß║Łc hai \(f\left( x \right)=-{{x}^{2}}-9x+10\). Tß║Łp hß╗Żp c├Īc gi├Ī trß╗ŗ cß╗¦a \(x\) ─æß╗ā \(f\left( x \right)\ge 0\) l├Ā
A. \(\left( -\infty ;-1\left] \cup \right[10;+\infty \right)\).
B. \(\left[ -1;10 \right]\).
C. \(\left[ -10;1 \right]\).
D. \(\left( -10;1 \right)\).
C├óu 4. Mß╗Öt kh├Īch sß║Īn c├│ 50 ph├▓ng. Hiß╗ćn tß║Īi mß╗Śi ph├▓ng cho thu├¬ vß╗øi gi├Ī 400 ngh├¼n ─æß╗ōng mß╗Öt ng├Āy th├¼ to├Ān bß╗Ö ph├▓ng ─æŲ░ß╗Żc thu├¬ hß║┐t. Biß║┐t rß║▒ng cß╗® mß╗Śi lß║¦n t─āng gi├Ī th├¬m 20 ngh├¼n ─æß╗ōng th├¼ c├│ th├¬m 2 ph├▓ng trß╗æng. Hß╗Åi ngŲ░ß╗Øi chß╗¦ kh├Īch sß║Īn cß║¦n chß╗Źn gi├Ī ph├▓ng mß╗øi l├Ā bao nhi├¬u ─æß╗ā doanh thu cß╗¦a kh├Īch sß║Īn trong ng├Āy l├Ā lß╗øn nhß║źt?
A. 480 ngh├¼n ─æß╗ōng.
B. 450 ngh├¼n ─æß╗ōng.
C. 500 ngh├¼n ─æß╗ōng.
D. 80 ngh├¼n ─æß╗ōng.
C├óu 5. C├│ bao nhi├¬u gi├Ī trß╗ŗ nguy├¬n cß╗¦a tham sß╗æ \(m\) ─æß╗ü h├Ām sß╗æ \(y=\sqrt{\left( m+1 \right){{x}^{2}}-2\left( m-1 \right)x+2-2m}\) c├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā \(\mathbb{R}\) ?
A. 3 .
B. 2 .
C. 1 .
D. 0 .
C├óu 6. Cho \(f\left( x \right)=a{{x}^{2}}+bx+c\left( a\ne 0 \right)\). ─Éiß╗üu kiß╗ćn ─æß╗ā \(f\left( x \right)<0,\forall x\in \mathbb{R}\) l├Ā:
A. \(\left\{ \begin{array}{*{35}{l}} a<0 \\ \text{ }\!\!\Delta\!\!\text{ }\le 0 \\ \end{array} \right.\).
B. \(\left\{ \begin{array}{*{35}{l}} a<0 \\ \text{ }\!\!\Delta\!\!\text{ }=0 \\ \end{array} \right.\).
C. \(\left\{ \begin{array}{*{35}{l}} a>0 \\ \text{ }\!\!\Delta\!\!\text{ }<0 \\ \end{array} \right.\).
D. \(\left\{ \begin{array}{*{35}{l}} a<0 \\ \text{ }\!\!\Delta\!\!\text{ }<0 \\ \end{array} \right.\).
C├óu 7. Cho \(f\left( x \right)=a{{x}^{2}}+bx+c\left( a\ne 0 \right)\) c├│ \(\text{ }\!\!\Delta\!\!\text{ }={{b}^{2}}-4ac<0\). Mß╗ćnh ─æß╗ü n├Āo ─æ├║ng?
A. \(f\left( x \right)>0,\forall x\in \mathbb{R}\).
B. \(f\left( x \right)<0,\forall x\in \mathbb{R}\).
C. \(f\left( x \right)\) kh├┤ng ─æß╗Ģi dß║źu.
D. Tß╗ōn tß║Īi \(x\) ─æß╗ā \(f\left( x \right)=0\).
C├óu 8. Tam thß╗®c bß║Łc hai \(f\left( x \right)=2{{x}^{2}}+2x+5\) nhß║Łn gi├Ī trß╗ŗ dŲ░ŲĪng khi v├Ā chß╗ē khi:
A. \(x\in \left( 0;+\infty \right)\).
B. \(x\in \left( -2;+\infty \right)\).
C. \(x\in \mathbb{R}\).
D. \(x\in \left( -\infty ;2 \right)\).
C├óu 9. Tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh \({{x}^{2}}-3x+2<0\) l├Ā:
A. \(\left( -\infty ;1 \right)\cup \left( 2;+\infty \right)\).
B. \(\left( 2;+\infty \right)\).
C. \(\left( 1;2 \right)\).
D. \(\left( -\infty ;1 \right)\).
C├óu 10. Sß╗æ thß╗▒c dŲ░ŲĪng lß╗øn nhß║źt thß╗Åa m├Żn \({{x}^{2}}-x-12\le 0\) l├Ā:
A. 1 .
B. 2 .
C. 3 .
D. 4 .
C├óu 11. Cho bß║źt phŲ░ŲĪng tr├¼nh \({{x}^{2}}-8x+7\ge 0\). Trong c├Īc tß║Łp hß╗Żp sau ─æ├óy, tß║Łp n├Āo c├│ chß╗®a phß║¦n tß╗Ł kh├┤ng phß║Żi l├Ā nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh?
A. \(\left( -\infty ;0 \right]\).
B. \(\left[ 8;+\infty \right)\).
C. \(\left( -\infty ;1 \right]\).
D. \(\left[ 6;+\infty \right)\).
C├óu 12. T├¼m tß║Łp x├Īc ─æß╗ŗnh \(D\) cß╗¦a h├Ām sß╗æ \(y=\sqrt{\frac{{{x}^{2}}+5x+4}{2{{x}^{2}}+3x+1}}\).
A. \(D=\left[ -4;-1 \right)\cup \left( -\frac{1}{2};+\infty \right)\).
B. \(D=\left( -\infty ;-4 \right]\cup \left( -1;-\frac{1}{2} \right)\).
C. \(D=\left( -\infty ;-4 \right)\cup \left( -\frac{1}{2};+\infty \right)\).
D. \(D=\left[ -4;-\frac{1}{2} \right)\).
C├óu 13. PhŲ░ŲĪng tr├¼nh \(\sqrt{f\left( x \right)}=g\left( x \right)\) tŲ░ŲĪng ─æŲ░ŲĪng vß╗øi phŲ░ŲĪng tr├¼nh n├Āo sau ─æ├óy?
A. \(\left\{ \begin{array}{*{35}{l}} f\left( x \right)\ge 0 \\ f\left( x \right)={{g}^{2}}\left( x \right) \\ \end{array} \right.\)
B. \(\left\{ \begin{array}{*{35}{l}} g\left( x \right)\ge 0 \\ f\left( x \right)={{g}^{2}}\left( x \right) \\ \end{array} \right.\)
C. \(\left[ \begin{array}{*{35}{l}} g\left( x \right)\ge 0 \\ f\left( x \right)={{g}^{2}}\left( x \right) \\ \end{array} \right.\)
D. \(f\left( x \right)={{g}^{2}}\left( x \right)\).
C├óu 14. Tß║Łp nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh \(\sqrt{2x+7}=x-4\) l├Ā
A. \(S=\left\{ 1;9 \right\}\).
B. \(S=\left\{ 1 \right\}\).
C. \(S=\left\{ 9 \right\}\).
D. \(S=\left\{ -1;-9 \right\}\).
C├óu 15. Tß║Łp nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh \(\sqrt{4{{x}^{2}}+x-6}=\sqrt{{{x}^{2}}+2x+4}\) l├Ā
A. \(S=\left\{ 2 \right\}\).
B. \(S=\left\{ -\frac{5}{3};2 \right\}\).
C. \(S=\left\{ -\frac{5}{3} \right\}\).
D. \(S=\varnothing \).
C├óu 16. PhŲ░ŲĪng tr├¼nh \(\left( x+5 \right)\left( 2-x \right)=3\sqrt{{{x}^{2}}+3x}\) c├│ tß╗Ģng b├¼nh phŲ░ŲĪng c├Īc nghiß╗ćm bß║▒ng:
A. 26.
B. 17 .
C. 10 .
D. 25 .
C├óu 17. PhŲ░ŲĪng tr├¼nh \(2\left( 1-x \right)\sqrt{{{x}^{2}}+2x-1}={{x}^{2}}-2x-1\) c├│ c├Īc nghiß╗ćm dß║Īng \(x=a\pm b\sqrt{c}\) trong ─æ├│ \(a\in \mathbb{Z},b,c\in \mathbb{N}\). T├Łnh tß╗Ģng \(a+b+c\).
A. 6 .
B. 0 .
C. 1 .
D. 3 .
---(Nß╗Öi dung ─æß║¦y ─æß╗¦ cß╗¦a phß║¦n trß║»c nghiß╗ćm vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
II. Tß╗▒ luß║Łn
C├óu 1. Mß╗Öt ngŲ░ß╗Øi muß╗æn uß╗æn tß║źm t├┤n phß║│ng h├¼nh chß╗» nhß║Łt c├│ bß╗ü ngang \(32\text{ }\!\!~\!\!\text{ cm}\), th├Ānh mß╗Öt r├Żnh dß║½n nŲ░ß╗øc bß║▒ng c├Īch chia tß║źm t├┤n ─æß╗æ th├Ānh ba phß║¦n rß╗ōi gß║źp hai b├¬n lß║Īi theo mß╗Öt g├│c vu├┤ng nhŲ░ h├¼nh vß║Į. Biß║┐t rß║▒ng diß╗ćn t├Łch mß║Ęt cß║»t ngang cß╗¦a r├Żnh nŲ░ß╗øc phß║Żi lß╗øn hŲĪn hoß║Ęc bß║▒ng tß╗Ģng \(120\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}\). Hß╗Åi ─æß╗Ö cao tß╗æi thiß╗āu v├Ā tß╗æi ─æa cß╗¦a r├Żnh dß║½n nŲ░ß╗øc l├Ā bao nhi├¬u cm?
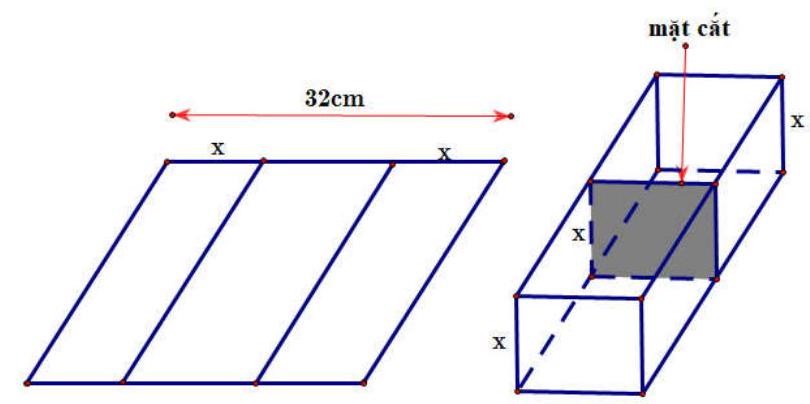
C├óu 2. Giß║Żi phŲ░ŲĪng tr├¼nh sau: \(\sqrt{{{x}^{2}}-3x+3}+\sqrt{{{x}^{2}}-3x+6}=3\);
C├óu 3. Cho \(A\left( 2;-4 \right),B\left( 6;0 \right),C\left( m;4 \right)\). ─Éß╗ŗnh \(m\) ─æß╗ā \(A,B,C\) thß║│ng h├Āng.
C├óu 4. Cho \(\Delta ABC\) c├│ trung ─æiß╗ām cß║Īnh \(BC\) l├Ā \(M\left( -1,-1 \right);AB:x+y-2=0;AC:2x+6y+3=0\). T├¼m 3 ─æiß╗ām \(A,B,C\).
III. ─É├Īp ├Īn
|
1C |
2B |
3C |
4C |
5B |
6D |
7C |
8C |
9C |
10D |
|
11D |
12C |
13B |
14C |
15B |
16B |
17A |
18C |
19C |
20B |
|
21D |
22D |
23D |
24A |
25A |
26B |
27B |
28B |
29A |
30A |
|
31A |
32D |
33C |
34C |
35A |
|
|
|
|
|
Tr├¬n ─æ├óy l├Ā mß╗Öt ph├ón tr├Łch dß║½n nß╗Öi dung ─Éß╗ü thi giß╗»a HK2 m├┤n To├Īn 10 CTST n─ām 2022-2023 TrŲ░ß╗Øng THPT Trß║¦n HŲ░ng ─Éß║Īo c├│ ─æ├Īp ├Īn. C├Īc em c├│ thß╗ā chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang HOC247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
C├Īc em c├│ thß╗ā tham khß║Żo th├¬m ─æß╗ü thi kh├Īc tß║Īi ─æ├óy:
- ─Éß╗ü thi giß╗»a HK2 m├┤n To├Īn 10 KNTT n─ām 2022-2023 TrŲ░ß╗Øng THPT L├¬ Qu├Į ─É├┤n c├│ ─æ├Īp ├Īn
- ─Éß╗ü thi giß╗»a HK2 m├┤n To├Īn 10 CD n─ām 2022-2023 TrŲ░ß╗Øng THPT L├Į Th├Īi Tß╗Ģ c├│ ─æ├Īp ├Īn
- ─Éß╗ü thi giß╗»a HK2 m├┤n To├Īn 10 CD n─ām 2022-2023 TrŲ░ß╗Øng THPT Nguyß╗ģn Thß╗ŗ Minh Khai c├│ ─æ├Īp ├Īn
Hy vß╗Źng ─æß╗ü thi n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong k├¼ thi sß║»p tß╗øi.













