Bộ 4 đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Kỳ Anh

TRƯỜNG THPT KỲ ANH

ĐỀ THI THPT QG NĂM HỌC 2021 MÔN: TOÁN Thời gian: 90 phút

Câu 1: Tính diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} - 2x\) và đường thẳng \(y = x.\)

A. \(\dfrac{9}{2}.\)

B. \(\dfrac{{11}}{6}.\)

C. \(\dfrac{{27}}{6}.\)

D. \(\dfrac{{17}}{6}.\)

Câu 2: Đồ thị hàm số nào dưới đây có tiệm cận ngang ?

A. \(y = {x^3} - x - 1.\)

B. \(y = \dfrac{{{x^3} + 1}}{{{x^2} + 1}}.\)

C. \(y = \dfrac{{{x^3} + 1}}{{{x^2} + 1}}.\)

D. \(y = \sqrt {2{x^2} + 3} .\)

Câu 3: Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a\) và cạnh bên bằng \(b\,\,\left( {a \ne b} \right).\) Phát biểu nào dưới đây SAI ?

A. Đoạn thẳng \(MN\) là đường vuông góc chung của \(AB\) và \(SC\) (\(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(SC\)).

B. Góc giữa các cạnh bên và mặt đáy bằng nhau.                 

C. Hình chiếu vuông góc của \(S\) trên mặt phẳng \(\left( {ABC} \right)\) là trọng tâm tam giác \(ABC.\)

D. \(SA\) vuông góc với \(BC.\)

Câu 4: Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(A'C'\) và \(BD\) bằng

A. \({60^0}.\)

B. \({30^0}.\)

C. \({45^0}.\)

D. \({90^0}.\)

Câu 5: Tính tích tất cả các nghiệm của phương trình \(\log _2^2x + {\log _2}x = \dfrac{{17}}{4}.\)

A. \(\dfrac{{17}}{4}.\)

B. \(\dfrac{1}{4}.\)

C. \(\dfrac{3}{2}.\)

D. \(\dfrac{1}{2}.\)

Câu 6: Cho \(a,\,\,b\) là hai số dương bất kì. Mệnh đề nào sau đây là ĐÚNG ?

A. \(\ln {a^b} = b\ln a.\)

B. \(\ln \left( {ab} \right) = \ln a.\ln b.\)

C. \(\ln \left( {a + b} \right) = \ln a + \ln b.\)

D. \(\ln \dfrac{a}{b} = \dfrac{{\ln a}}{{\ln b}}.\)

Câu 7: Tích phân \(I = \int\limits_0^1 {{e^{x\, + \,1}}\,{\rm{d}}x} \) bằng

A. \({e^2} - 1.\)

B. \({e^2} - e.\)

C. \({e^2} + e.\)

D. \(e - {e^2}.\)

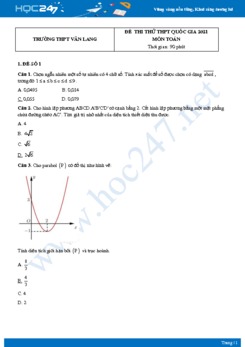
Câu 8: Cho hàm số \(f\left( x \right)\) liên trục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào ?

A. \(\left( { - \,\infty ;0} \right).\)

B. \(\left( { - \,\infty ; - \,1} \right).\)

C. \(\left( {1; + \,\infty } \right).\)

D. \(\left( { - \,1;1} \right).\)

Câu 9: \(\mathop {\lim }\limits_{x\, \to \, - \,\infty } \dfrac{{3x - 1}}{{x + 5}}\) bằng

A. \(3.\)

B. \( - \,3.\)

C. \( - \dfrac{1}{5}.\)

D. \(5.\)

Câu 10: Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ.

A. \(\dfrac{2}{3}.\)

B. \(\dfrac{{17}}{{48}}.\)

C. \(\dfrac{{17}}{{24}}.\)

D. \(\dfrac{4}{9}.\)

ĐÁP ÁN

1. A	2. C	3. A	4. D	5. D
6. A	7. B	8. C	9. A	10. C

{-- Nội dung đề, đáp án từ câu 11-50 các em vui lòng xem ở phần xem online hoặc tải về --}

Câu 1: Trong không gian với hệ tọa độ \(Oxyz,\) cho đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{y}{1} = \dfrac{{z + 2}}{1}\) và điểm \(M\left( {2; - \,1;0} \right).\) Gọi \(\left( S \right)\) là mặt cầu có tâm \(I\) thuộc đường thẳng \(d\) và tiếp xúc với \(mp\,\,\left( {Oxy} \right)\) tại điểm \(M.\) Hỏi có bao nhiêu mặt cầu thỏa mãn ?

A. 2.

B. 1.

C. 0.

D. Vô số.

Câu 2: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

A. \(y = {x^3} - 3x.\)

B. \(y =  - \,{x^3} + 3x.\)

C. \(y = {x^4} - 2{x^2}.\)

D. \(y = {x^3} - {x^2}.\)

Câu 3: Cho số phức \(z = a + bi\) (\(a,\,\,b\) là các số thực) thỏa mãn \(z.\left| z \right| + 2z + i = 0.\) Tính giá trị của biểu thức \(T = a + {b^2}.\)

A. \(T = 4\sqrt 3  - 2.\)

B. \(T = 3 + 2\sqrt 2 .\)

C. \(T = 3 - 2\sqrt 2 .\)

D. \(T = 4 + 2\sqrt 3 .\)

Câu 4: Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là

A. \(10!.\)

B. \({10^2}.\)

C. \({2^{10}}.\)

D. \({10^{10}}.\)

Câu 5: Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right).\) Biết \(SA = 2a\) và tam giác \(ABC\) vuông tại \(A\) có \(AB = 3a,\,\,AC = 4a.\) Tính thể tích khối chóp \(S.ABC\) theo \(a.\)

A. \(12{a^3}.\)

B. \(6{a^3}.\)

C. \(8{a^3}.\)

D. \(4{a^3}.\)

Câu 6: Họ nguyên hàm của hàm số \(f\left( x \right) = \sin 5x + 2\) là

A. \(5\cos 5x + C.\)

B. \( - \dfrac{1}{5}\cos 5x + 2x + C.\)

C. \(\dfrac{1}{5}\cos 5x + 2x + C.\)

D. \(\cos 5x + 2x + C.\)

Câu 7: Tập nghiệm của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{2x\, - \,1}} \ge \dfrac{1}{3}\) là

A. \(\left( { - \,\infty ;0} \right].\)

B. \(\left( {0;1} \right].\)

C. \(\left[ {1; + \,\infty } \right).\)

D. \(\left( { - \,\infty ;1} \right].\)

Câu 8: Giá trị nhỏ nhất của hàm số \(y = {x^3} + 3{x^2} - 9x + 1\) trên đoạn \(\left[ { - \,4;4} \right]\) là

A. \( - \,4.\)

B. \(4.\)

C. \(1.\)

D. \( - \,1.\)

Câu 9: Gọi \({z_1},\,\,{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 6z + 13 = 0\) trong đó \({z_1}\) là số phức có phần ảo âm. Tìm số phức \(\omega  = {z_1} + 2{z_2}.\)

A. \(\omega  = 9 + 2i.\)

B. \(\omega  =  - \,9 + 2i.\)

C. \(\omega  =  - \,9 - 2i.\)

D. \(\omega  = 9 - 2i.\)

Câu 10: Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng \(\left( P \right):y - 2z + 1 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)\) ?

A. \(\vec n = \left( {1; - \,2;1} \right).\)

B. \(\vec n = \left( {1; - \,2;0} \right).\)

C. \(\vec n = \left( {0;1; - \,2} \right).\)

D. \(\vec n = \left( {0;2;4} \right).\)

ĐÁP ÁN

1. B	2. A	3. C	4. A	5. D
6. B	7. D	8. A	9. B	10. C

{-- Nội dung đề, đáp án từ câu 11-50 các em vui lòng xem ở phần xem online hoặc tải về --}

Câu 1: Trong không gian với hệ tọa độ \(Oxyz,\) cho đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{{ - \,2}} = \dfrac{{z - 1}}{2}.\) Điểm nào dưới đây KHÔNG thuộc \(d\) ?

A. \(E\left( {2; - \,2;3} \right).\)

B. \(N\left( {1;0;1} \right).\)

C. \(F\left( {3; - \,4;5} \right).\)

D. \(M\left( {0;2;1} \right).\)

Câu 2: Cho hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right].\) Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi hai đồ thị \(y = f\left( x \right),\,\,y = g\left( x \right)\) và các đường thẳng \(x = a,\,\,x = b.\) Diện tích \(\left( H \right)\) được tính theo công thức

A. \({S_H} = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x}  - \int\limits_a^b {\left| {g\left( x \right)} \right|{\rm{d}}x} .\)

B. \({S_H} = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|{\rm{d}}x} .\)

C. \({S_H} = \left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]{\rm{d}}x} } \right|.\)

D. \({S_H} = \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]{\rm{d}}x} .\)

Câu 3: Tìm hệ số của số hạng chứa \({x^{10}}\) trong khai triển của biểu thức \({\left( {3{x^3} - \dfrac{2}{{{x^2}}}} \right)^5}.\)

A. \( - \,810.\)

B. \(826.\)

C. \(810.\)

D. \(421.\)

Câu 4: Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 2} \right)^2} = 9\) và mặt phẳng \(\left( P \right):2x - y - 2z + 1 = 0.\) Biết \(\left( P \right)\) cắt \(\left( S \right)\) theo giao tuyến là đường tròn có bán kính \(r.\) Tính \(r.\)

A. \(r = 3.\)

B. \(r = 2\sqrt 2 .\)

C. \(r = \sqrt 3 .\)

D. \(r = 2.\)

Câu 5: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Giá trị cực tiểu của hàm số bằng

A. \(1.\)

B. \(3.\)

C. \(3.\)

D. \( - \,1.\)

Câu 6: Cho hình trụ có chiều cao \(h\) và bán kính đáy \(R.\) Công thức tính thể tích của khối trụ là

A. \(\pi R{h^2}.\)

B. \(\pi {R^2}h.\)

C. \(\dfrac{1}{3}\pi R{h^2}.\)

D. \(\dfrac{1}{3}\pi {R^2}h.\)

Câu 7: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Số nghiệm của phương trình \(f\left( x \right) + 3 = 0\) là

A. 0.

B. 3.

C. 2.

D. 1.

Câu 8: Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(M\left( {1;0;4} \right)\) và đường thẳng \(d\) có phương trình là \(\dfrac{x}{1} = \dfrac{{y - 1}}{{ - \,1}} = \dfrac{{z + 1}}{2}.\) Tìm hình chiếu vuông góc \(H\) của \(M\) lên đường thẳng \(d.\)

A. \(H\left( {1;0;1} \right).\)

B. \(H\left( { - \,2;3;0} \right).\)

C. \(H\left( {0;1; - \,1} \right).\)

D. \(H\left( {2; - \,1;3} \right).\)

Câu 9: Biết \(I = \int\limits_0^1 {\dfrac{x}{{\sqrt {3x + 1}  + \sqrt {2x + 1} }}\,{\rm{d}}x}  = \dfrac{{a + b\sqrt 3 }}{9},\) với \(a,\,\,b\) là các số thực. Tính tổng \(T = a + b.\)

A. \(T =  - \,10.\)

B. \(T =  - \,4.\)

C. \(T = 15.\)

D. \(T = 8.\)

Câu 10: Ông V gửi tiết kiệm 200 triệu đồng vào ngân hàng với hình thức lãi kép và lãi suất 7,2% một năm. Hỏi sau 5 năm ông V thu về số tiền (cả vốn lẫn lãi) gần nhất với số nào sau đây ?

A. 283.145.000 đồng.

B. 283.155.000 đồng.            

C. 283.142.000 đồng.

D. 283.151.000 đồng.

ĐÁP ÁN

1. D	2. B	3. A	4. B	5. A
6. B	7. C	8. D	9. D	10. C

{-- Nội dung đề, đáp án từ câu 11-50 các em vui lòng xem ở phần xem online hoặc tải về --}

Câu 1: Cho số phức \(z = 3 + 2i.\) Tính \(\left| z \right|.\)

A. \(\left| z \right| = \sqrt 5 .\)

B. \(\left| z \right| = \sqrt {13} .\)

C. \(\left| z \right| = 5.\)

D. \(\left| z \right| = 13.\)

Câu 2: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a,\) mặt bên \(SAB\) là tam giác vuông cân tại \(S\) và nằm trên mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng \(AB\) và \(SC.\)

A. \(\dfrac{{a\sqrt 3 }}{3}.\)

B. \(\dfrac{{a\sqrt 5 }}{5}.\)

C. \(\dfrac{{2a\sqrt 3 }}{3}.\)

D. \(\dfrac{{2a\sqrt 5 }}{5}.\)

Câu 3: Cho mặt cầu \(\left( S \right)\) bán kính \(R = 5\,\,cm.\) Mặt phẳng \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có chu vi bằng \(8\pi \,\,cm.\) Bốn điểm \(A,\,\,B,\,\,C,\,\,D\) thay đổi sao cho \(A,\,\,B,\,\,C\) thuộc đường tròn \(\left( C \right),\) điểm \(D\) thuộc \(\left( S \right)\) (không thuộc đường tròn \(\left( C \right)\)) và tam giác \(ABC\) là tam giác đều. Tính thể tích lớn nhất của tứ diện \(ABCD.\)

A. \(32\sqrt 3 \,\,c{m^3}.\)

B. \(60\sqrt 3 \,\,c{m^3}.\)

C. \(20\sqrt 3 \,\,c{m^3}.\)

D. \(96\sqrt 3 \,\,c{m^3}.\)

Câu 4: Gọi \(S = \left( {a;b} \right)\) là tập tất cả các giá trị của tham số thực \(m\) để phương trình

\({\log _2}\left( {mx - 6{x^3}} \right) + {\log _{\dfrac{1}{2}}}\left( { - \,14{x^2} + 29x - 2} \right) = 0\)

có 3 nghiệm phân biệt. Khi đó hiệu \(H = b - a\) bằng

A. \(\dfrac{5}{2}.\)

B. \(\dfrac{1}{2}.\)

C. \(\dfrac{2}{3}.\)

D. \(\dfrac{5}{3}.\)

Câu 5: Có bao nhiêu giá trị nguyên của \(m\) để phương trình \({2^{{{\sin }^2}x}} + {3^{{{\cos }^2}x}} = m{.3^{{{\sin }^2}x}}\) có nghiệm ?

A. 7.

B. 4.

C. 5.

D. 6.

Câu 6: Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_n} = {u_{n\, - \,1}} + 6,\,\,\forall n \ge 2\) và \({\log _2}{u_5} + {\log _{\sqrt 2 }}\sqrt {{u_9} + 8}  = 11.\)

Đặt \({S_n} = {u_1} + {u_2} + \,\,...\,\, + {u_n}.\) Tìm số tự nhiên \(n\) nhỏ nhất thỏa mãn \({S_n} \ge 20172018.\)

A. 2587.

B. 2590.

C. 2593.

D. 2584.

Câu 7: Cho hàm số \(f\left( x \right) = {x^4} + 4m{x^3} + 3\left( {m + 1} \right){x^2} + 1.\) Gọi \(S\) là tập hợp tất cả các giá trị nguyên của \(m\) để hàm số có cực tiểu mà không có cực đại. Tính tổng các phần tử của tập \(S.\)

A. 1.

B. 2.

C. 6.

D. 0.

Câu 8: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a,\,\,BD = a.\) Cạnh bên \(SA\) vuông góc với mặt đáy và \(SA = \dfrac{{a\sqrt 6 }}{2}.\) Tính góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {SCD} \right).\)

A. \({60^0}.\)

B. \({120^0}.\)

C. \({45^0}.\)

D. \({90^0}.\)

Câu 9: Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 4\) và một điểm \(M\left( {2;3;1} \right).\) Từ \(M\) kẻ được vô số các tiếp tuyến tới \(\left( S \right),\) biết tập hợp các tiếp điểm là đường tròn \(\left( C \right).\) Tính bán kính \(r\) của đường tròn \(\left( C \right).\)

A. \(r = \dfrac{{2\sqrt 3 }}{3}.\)

B. \(r = \dfrac{{\sqrt 3 }}{3}.\)

C. \(r = \dfrac{{\sqrt 2 }}{3}.\)

D. \(r = \dfrac{{\sqrt 3 }}{2}.\)

Câu 10: Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng \(\left( P \right):2x - 2y + z = 0\) và đường thẳng \(d:\dfrac{{x + 1}}{1} = \dfrac{y}{2} = \dfrac{z}{{ - \,1}}.\) Gọi \(\Delta \) là một đường thẳng chứa trong \(\left( P \right)\) cắt và vuông góc với \(d.\) Vectơ \(\vec u = \left( {a;1;b} \right)\) lf một vectơ chỉ phương của \(\Delta .\) Tính tổng \(S = a + b.\)

A. \(S = 1.\)

B. \(S = 0.\)

C. \(S = 2.\)

D. \(S = 4.\)

ĐÁP ÁN

1. B	2. D	3. A	4. B	5. B
6. C	7. A	8. D	9. A	10. C

{-- Nội dung đề, đáp án từ câu 11-50 các em vui lòng xem ở phần xem online hoặc tải về --}

Trên đây là trích dẫn 1 phần nội dung tài liệu Bộ 4 đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Kỳ Anh. Để xem toàn bộ nội dung các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập .

Các em quan tâm có thể tham khảo thêm các tài liệu cùng chuyên mục:

• Bộ 4 đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Tam Phước

• Bộ 4 đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thái Thuận

• Bộ 4 đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Hàm Yên

​Chúc các em học tập tốt !