Phần hướng dẫn giải bài tập SGK Hình học 9 Bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9.
-
Bài tập 12 trang 106 SGK Toán 9 Tập 1
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8 cm
a) Tính khoảng cách từ tâm O đến dây AB
b) Gọi I là điểm thuộc dây AB sao cho AI=1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD=AB.
-
Bài tập 13 trang 106 SGK Toán 9 Tập 1
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:
a) EH=EK
b) EA=EC
-
Bài tập 14 trang 106 SGK Toán 9 Tập 1
Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.
-
Bài tập 15 trang 106 SGK Toán 9 Tập 1
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết \(AB> CD\).
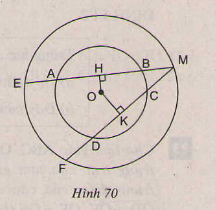
Hãy so sánh các độ dài:
a) OH và OK
b) ME và MF
c) MH và MK
-
Bài tập 16 trang 106 SGK Toán 9 Tập 1
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
-
Bài tập 24 trang 160 SBT Toán 9 Tập 1
Cho hình \(74,\) trong đó \(MN = PQ.\) Chứng minh rằng:
\(a)\) \(AE = AF\)
\(b)\) \(AN = AQ.\)
-
Bài tập 25 trang 160 SBT Toán 9 Tập 1
Cho hình \(75,\) trong đó hai dây \(CD, EF\) bằng nhau và vuông góc với nhau tại \(I,\) \(IC = 2cm,\) \(ID = 14cm.\) Tính khoảng cách từ \(O\) đến mỗi dây.
-
Bài tập 26 trang 160 SBT Toán 9 Tập 1
Cho đường tròn \((O),\) dây \(AB\) và dây \(CD,\) \(AB < CD.\) Giao điểm \(K\) của các đường thẳng \(AB,\) \(CD\) nằm ngoài đường tròn. Đường tròn \((O ; OK)\) cắt \(KA\) và \(KC\) tại \(M\) và \(N.\) Chứng minh rằng \(KM < KN.\)
-
Bài tập 27 trang 160 SBT Toán 9 Tập 1
Cho đường tròn \((O)\) và điểm \(I\) nằm bên trong đường tròn. Chứng minh rằng dây \(AB\) vuông góc với \(OI\) tại \(I\) ngắn hơn mọi dây khác đi qua \(I.\)
-
Bài tập 28 trang 160 SBT Toán 9 Tập 1
Tam giác \(ABC\) nội tiếp đường tròn \((O)\) có \(\widehat A > \widehat B > \widehat C.\) Gọi \(OH, OI, OK\) theo thứ tự là khoảng cách từ \(O\) đến \(BC,\)\( AC,\)\( AB.\) So sánh các độ dài \(OH, OI, OK.\)
-
Bài tập 29 trang 161 SBT Toán 9 Tập 1
Cho đường tròn \((O),\) hai dây \(AB, CD\) bằng nhau và cắt nhau tại điểm \(I\) nằm bên trong đường tròn. Chứng minh rằng:
\(a)\) \(IO\) là tia phân giác của một trong hai góc tạo bởi hai dây \(AB\) và \(CD.\)
\(b)\) Điểm \(I\) chia \(AB,\) \(CD\) thành các đoạn thẳng bằng nhau đôi một.
-
Bài tập 30 trang 161 SBT Toán 9 Tập 1
Cho đường tròn tâm \(O\) bán kính \(25cm.\) Hai dây \(AB, CD\) song song với nhau và có độ dài theo thứ tự bằng \(40cm,\) \(48cm.\) Tính khoảng cách giữa hai dây ấy.
-
Bài tập 31 trang 161 SBT Toán 9 Tập 1
Cho đường tròn \((O),\) các bán kính \(OA\) và \(OB.\) Trên cung nhỏ \(AB\) lấy các điểm \(M\) và \(N\) sao cho \(AM = BN.\) Gọi \(C\) là giao điểm của các đường thẳng \(AM\) và \(BN.\) Chứng minh rằng:
\(a)\) \(OC\) là tia phân giác của góc \(AOB.\)
\(b)\) \(OC\) vuông góc với \(AB.\)
-
Bài tập 32 trang 161 SBT Toán 9 Tập 1
Cho đường tròn tâm \(O\) bán kính \(5dm,\) điểm \(M\) cách \(O\) là \(3dm.\)
\(a)\) Tính độ dài dây ngắn nhất đi qua điểm \(M.\)
\(b)\) Tính độ dài dây dài nhất đi qua \(M.\)
-
Bài tập 34 trang 161 SBT Toán 9 Tập 1
Cho đường tròn \((O)\) và hai điểm \(A, B\) nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm \(A\) nằm trên một dây, điểm \(B\) nằm trên dây còn lại.
-
Bài tập 3.1 trang 161 SBT Toán 9 Tập 1
Cho đường tròn (O) đường kính 6cm, dây AB bằng 2cm. Khoảng cách từ O đến AB bằng
A. \(\sqrt {35} \) cm;
B. \(\sqrt {5} \) cm;
C. 4\(\sqrt {2} \) cm;
D. 2\(\sqrt {2} \) cm.
Hãy chọn phương án đúng.
-
Bài tập 3.2 trang 161 SBT Toán 9 Tập 1
Cho đường tròn \((O),\) điểm \(I\) nằm bên trong đường tròn \((\) \(I\) khác \(O).\) Dựng dây \(AB\) đi qua \(I\) và có độ dài ngắn nhất.
-
Bài tập 3.3 trang 161 SBT Toán 9 Tập 1
Cho đường tròn \((O ; 25cm),\) điểm \(C\) cách \(O\) là \(7cm.\) Có bao nhiêu dây đi qua \(C\) có độ dài là một số nguyên xentimét\(?\)
-
Bài tập 33 trang 161 SBT Toán 9 Tập 1
Cho đường tròn \((O),\) hai dây \(AB\) và \(CD\) cắt nhau tại điểm \(M\) nằm bên trong đường tròn. Gọi \(H\) và \(K\) theo thứ tự là trung điểm của \(AB\) và \(CD.\) Cho biết \(AB >CD,\) chứng minh rằng \(MH > MK.\)






