Bài tập 92 trang 121 SBT Toán 9 Tập 1
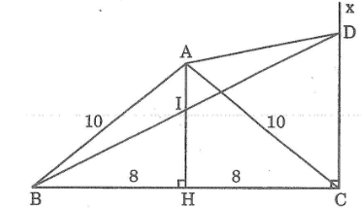
Cho tam giác ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho AI =\(\frac{1}{3}\).AH. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D
a. Tính các góc của tam giác ABC
b. Tính diện tích tứ giác ABCD
Hướng dẫn giải chi tiết
a. Ta có: AH ⊥ BC, suy ra: HB = HC = BC/2 = 8 (cm)
Trong tam giác vuông ABH, ta có:
b. Áp dụng định lí Pi-ta-go vào tam giác vuông ABH ta có:
AB2 = AH2 + BH2 ⇒ AH2 = AB2 – BH2= 102 – 82 = 36
Suy ra: AH = 6 (cm)
Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)
Vì IH ⊥ BC và DC ⊥ BC nên IH // DC (1)
-- Mod Toán 9 HỌC247
-


Tính độ dài AB, biết BC = 25cm, DK = 6cm
bởi Ha Ku
 26/01/2019
26/01/2019
Cho tam giác ABC vuông tại A, đường cao AH. Tia phân giác của góc HAC cắt HC tại D. Gọi K là hình chiếu của D trên AC. Biết BC = 25cm, DK = 6cm. Tính độ dài AB
Theo dõi (0) 1 Trả lời -


1: tam giác ABC vuông tại A . Cạnh AB =3 ,AC = 4 . Tính tỉ số lượng giác của góc B và C
2: tam giác ABC vuông tại A . Cạnh AB = 12 , BC = 13 . Tính tỉ số lượng giác của góc B ,C
3: cho tam giác MPQ vuông tại M. Cạnh MP = 8 , PQ = 10 . Tính tỉ số lượng giác của góc P ,Q
Theo dõi (0) 1 Trả lời -


Chứng minh tan^2α−sin^2α⋅tan^2α=sin^2α
bởi Thuy Kim
 28/01/2019
28/01/2019
GIÚP DÙM MÌNH NHA MÌNH ĐANG CẦN GẤP ^^
1/Chứng minh:
a)\(\tan^2\alpha-\sin^2\alpha\cdot tan^2\alpha=sin^2\alpha\)
b) \(\cos^2\alpha+\tan^2\alpha\cdot\cos^2\alpha=1\)
2/Cho tam giác ABC có BH là đường cao, biết AB = 40cm;AC=58cm;BC=42cm
a) Chứng minh tam giác ABC vuông
b) Tính tỉ số lượng giác của \(\widehat{A}\)
C)Vẽ HE⊥AB;HF⊥BC. Tính BH ; BE; BF và \(S_{EFCA}\)
Theo dõi (0) 1 Trả lời -


Tính AB, AC, BC, CH, biết AH= 14cm, HB/HC =1/4
bởi Dương Quá
 26/01/2019
26/01/2019
cho tam giác abc vuông tại A ,đường cao AH biết AH= 14cm , HB/HC =1/4. TÍNH AB,AC,BC,CH.
Theo dõi (0) 1 Trả lời -


Tính BC và BD biết AD=12 cm, CD=25cm
bởi Đào Lê Hương Quỳnh
 28/01/2019
28/01/2019
Cho hình thang ABCD vuông ( góc A= góc B= 90 độ). Đường chéo BD vuông góc với BC. Tính BC và BD biết AD=12 cm, CD=25cm.
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của BE^2 + CF^2
bởi Tuấn Huy
 26/01/2019
26/01/2019
Cho tam giác ABC vuông tại A có đường cao AH. Gọi HE và HF lần lượt là các đường cao của tam giác AHB và AHC. Chứng minh:
a) \(BC^2=3AH^2+BE^2+CF^2\).
b) Giả sử BC = 2a là độ dài cố định. Tìm giá trị nhỏ nhất của \(BE^2+CF^2\).
Theo dõi (0) 1 Trả lời -


Chứng minh rằng AB^2 = BD^2 − DC^2
bởi Nguyễn Vũ Khúc
 26/01/2019
26/01/2019
Cho tam giác ABC vuông tại A có M là trung điểm của AC. Kẻ MD vuông góc với BC tại D. Chứng minh rằng: \(AB^2=BD^2-DC^2\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng AB.AM = AC.AN
bởi Nguyễn Thanh Hà
 26/01/2019
26/01/2019
Cho tam giác ABC có đường cao AH. Gọi M và N là hình chiếu của H lên cạnh AB và AC. Chứng minh rằng: AB.AM = AC.AN
Theo dõi (0) 1 Trả lời -


Chứng tỏ AH^3= BC.BE.CF=BC.HE.AF
bởi Mai Hoa
 28/01/2019
28/01/2019
Cho tam giác ABC vuông tại A, đường cao AH.Gọi E,H lần lượt là hình chiếu vuông góc của H lên AH,AC, Đặt AH=x,BC=2a(a là hằng số).
a) Chứng tỏ AH3= BC.BE.CF=BC.HE.AF
b) tính AEF theo a và x. Tính x để diện tích AEF đạt giá trị lớn nhất
Theo dõi (0) 1 Trả lời -


Tìm các cạnh chưa biết của tam giác, biết hai cạnh góc vuông AB = 6 và AC = 8
bởi Mai Vàng
 28/01/2019
28/01/2019
Cho tam giác ABC vuông tại A. Tìm các cạnh chưa biết của tam giác, biết:
a) Hai cạnh góc vuông AB = 6 và AC = 8.
b) Cạnh góc vuông AB = 24 và cạnh huyền BC = 30.
c) Đường cao AH = 12 và hình chiếu BH = 16.
d) Đường cao AH = 2,4 và cạnh AB = 4.
e) Hình chiếu BH = 9 và CH = 16.
f) Cạnh góc vuông AB = 15 và \(\dfrac{AB}{AC}=\dfrac{3}{4}\).
g) Đường cao AH = 12 và \(\dfrac{AB}{AC}=\dfrac{3}{4}\).
h) Đường cao AH = 12 và cạnh huyền BC = 25.
i) Cạnh góc vuông AB = 1 và CH = 1,5.
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 1/BK^2=1/BC^2+1/4AH^2
bởi Tram Anh
 28/01/2019
28/01/2019
Cho tam giác ABC cân tại A có các đường cao AH và BK . CM \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 90 trang 121 SBT Toán 9 Tập 1
Bài tập 91 trang 121 SBT Toán 9 Tập 1
Bài tập 93 trang 121 SBT Toán 9 Tập 1
Bài tập 94 trang 122 SBT Toán 9 Tập 1
Bài tập 95 trang 122 SBT Toán 9 Tập 1
Bài tập 96 trang 122 SBT Toán 9 Tập 1
Bài tập 97 trang 122 SBT Toán 9 Tập 1
Bài tập 98 trang 122 SBT Toán 9 Tập 1
Câu hỏi 1 trang 91 SGK Toán 9 Tập 1
Câu hỏi 2 trang 91 SGK Toán 9 Tập 1
Câu hỏi 3 trang 91 SGK Toán 9 Tập 1
Câu hỏi 4 trang 91 SGK Toán 9 Tập 1
Bài tập 33 trang 93 SGK Toán 9 Tập 1
Bài tập 34 trang 93 SGK Toán 9 Tập 1
Bài tập 35 trang 94 SGK Toán 9 Tập 1
Bài tập 36 trang 94 SGK Toán 9 Tập 1
Bài tập 37 trang 94 SGK Toán 9 Tập 1
Bài tập 38 trang 95 SGK Toán 9 Tập 1
Bài tập 39 trang 95 SGK Toán 9 Tập 1
Bài tập 40 trang 95 SGK Toán 9 Tập 1
Bài tập 41 trang 96 SGK Toán 9 Tập 1