Bài tập 63 trang 115 SBT Toán 9 Tập 1
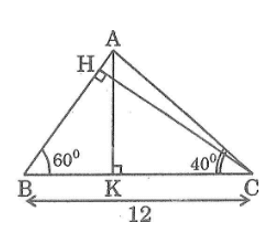
Cho tam giác ABC có BC = 12cm, góc B = 600, góc C = 400. Tính:
a. Đường cao CH và cạnh AC
b. Diện tích tam giác ABC
Hướng dẫn giải chi tiết
-- Mod Toán 9 HỌC247
-


Tính MN, MP, NP, biết MH= 6cm, NH= 4,5cm
bởi minh thuận
 26/01/2019
26/01/2019
cho tam giác vuông MNP tại M, đường cao MH. Biết MH= 6cm, NH= 4,5cm.
Tính MN, MP, NP
Theo dõi (0) 1 Trả lời -


Tính HB, HC có đường cao AH, A/B = 3/7, AH=48 cm
bởi Phạm Phú Lộc Nữ
 26/01/2019
26/01/2019
Cho tam giác vuông ABC, đường cao AH, \(\dfrac{A}{B}=\dfrac{3}{7}\) AH=48 cm
Tính HB, HC
Theo dõi (0) 1 Trả lời -


Tính độ dài các cạnh AC, BC, AH, cho AB=15cm và HC=16cm
bởi Mai Rừng
 26/01/2019
26/01/2019
cho tam giác ABC vuông tại A. kẻ AH vuông góc với BC. cho AB=15cm và HC=16cm tính độ dài các cạnh AC, BC, AH?
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 1/AB^2=1/AE^2+1/4AF^2
bởi Suong dem
 26/01/2019
26/01/2019
cho hình chữ nhật ABCD,AB=2BC. Trên cạnh BC lấy điểm E. Tia AE cắt đường thẳng CD tại F. Cmr: \(\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{4AF^2}\)
bạn nào bt lm giúp mik vs nhé
Theo dõi (0) 1 Trả lời -


Chứng minh AH.DH = BH.EH = CH.FH
bởi Quynh Nhu
 26/01/2019
26/01/2019
Cho tam giác ABC có góc nhọn, các đường cao AD, BE và CF cắt nhau tại H.
a) Chứng minh: AE.AC = AF.AB => \(\Delta\)ABC và \(\Delta\)AEF đồng dạng.
b) Chứng minh: AH.DH = BH.EH = CH.FH.
c) Chứng minh DA là tia phân giác của \(\widehat{EDF}\)
d) Chứng minh: SABC = \(\dfrac{1}{2}\).AB.AC.sinA. Từ đó
=> \(\dfrac{S_{DEF}}{S_{ABC}}=1-\)(cos2A + cos2B + cos2C)
e) Chứng minh: \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{BF}=1\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 61 trang 115 SBT Toán 9 Tập 1
Bài tập 62 trang 115 SBT Toán 9 Tập 1
Bài tập 65 trang 115 SBT Toán 9 Tập 1
Bài tập 66 trang 115 SBT Toán 9 Tập 1
Bài tập 67 trang 115 SBT Toán 9 Tập 1
Bài tập 68 trang 116 SBT Toán 9 Tập 1
Bài tập 69 trang 116 SBT Toán 9 Tập 1
Bài tập 70 trang 116 SBT Toán 9 Tập 1
Bài tập 71 trang 116 SBT Toán 9 Tập 1
Bài tập 4.1 trang 116 SBT Toán 9 Tập 1
Bài tập 4.2 trang 116 SBT Toán 9 Tập 1
Bài tập 4.3 trang 117 SBT Toán 9 Tập 1
Bài tập 4.4 trang 117 SBT Toán 9 Tập 1
Bài tập 4.4 trang 117 SBT Toán 9 Tập 1
Bài tập 4.6 trang 117 SBT Toán 9 Tập 1