Giải bài 58 tr 61 sách BT Toán lớp 9 Tập 2
Hà Nội cách Nam Định \(90km\). Hai ô tô khởi hành đồng thời, xe thứ nhất từ Hà Nội, xe thứ hai từ Nam Định và đi ngược chiều nhau. Sau \(1\) giờ chúng gặp nhau. Tiếp tục đi, xe thứ hai tới Hà Nội trước khi xe thứ nhất tới Nam Định là \(27\) phút. Tính vận tốc mỗi xe.
Hướng dẫn giải chi tiết
Hướng dẫn giải
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải chi tiết
Gọi vận tốc xe thứ nhất là \(\displaystyle x (km/h)\); điều kiện: \(\displaystyle 0< x < 90\)
Vì sau \(\displaystyle 1\) giờ hai xe gặp nhau, vậy quãng đường hai xe đi được trong một giờ là \(\displaystyle 90 km\) tức tổng vận tốc của hai xe là \(\displaystyle 90km/h\) nên vận tốc của xe thứ hai đi là \(\displaystyle 90 – x (km/h)\)
Quãng đường xe thứ nhất tiếp tục đi là: \(\displaystyle 90 – x (km)\)
Thời gian xe thứ nhất đi đoạn đường còn lại là \(\displaystyle {{90 - x} \over x}\) giờ
Quãng đường xe thứ hai tiếp tục đi là \(\displaystyle x (km)\)
Thời gian xe thứ hai đi đoạn còn lại là \(\displaystyle {x \over {90 - x}}\) giờ
Xe thứ hai đến Hà Nội trước xe thứ nhất đến Nam Định là \(\displaystyle 27\) phút bằng \(\displaystyle {9 \over {20}}\) giờ.
Ta có phương trình:
\(\displaystyle \eqalign{
& {{90 - x} \over x} - {x \over {90 - x}} = {9 \over {20}} \cr
& \Rightarrow 20{\left( {90 - x} \right)^2} - 20{x^2} = 9x\left( {90 - x} \right) \cr
& \Leftrightarrow 20\left( {8100 - 180x + {x^2}} \right) - 20{x^2} = 810x - 9{x^2} \cr
& \Leftrightarrow 162000 - 3600x + 20{x^2} - 20{x^2} - 810x + 9{x^2} = 0 \cr
& \Leftrightarrow 9{x^2} - 4410x + 162000 = 0 \cr
& \Leftrightarrow {x^2} - 490x + 18000 = 0 \cr
& \Delta ' = (-245)^2 - 1.18000 = 42025 > 0 \cr
& \sqrt {\Delta '} = \sqrt {42025} = 205 \cr
& {x_1} = {{245 + 205} \over 1} = 450 \cr
& {x_2} = {{245 - 205} \over 1} = 40 \cr} \)
\(\displaystyle x_2= 450 > 90\) không thỏa mãn điều kiện: loại.
Vậy: vận tốc xe thứ nhất là \(\displaystyle 40km/h\)
Vận tốc xe thứ hai là \(\displaystyle 90 - 40 = 50\) km/h
-- Mod Toán 9 HỌC247
-


Tìm vận tốc riêng của canô trên khúc sông dài 80km
bởi Ngát Ngô
 14/03/2020
14/03/2020
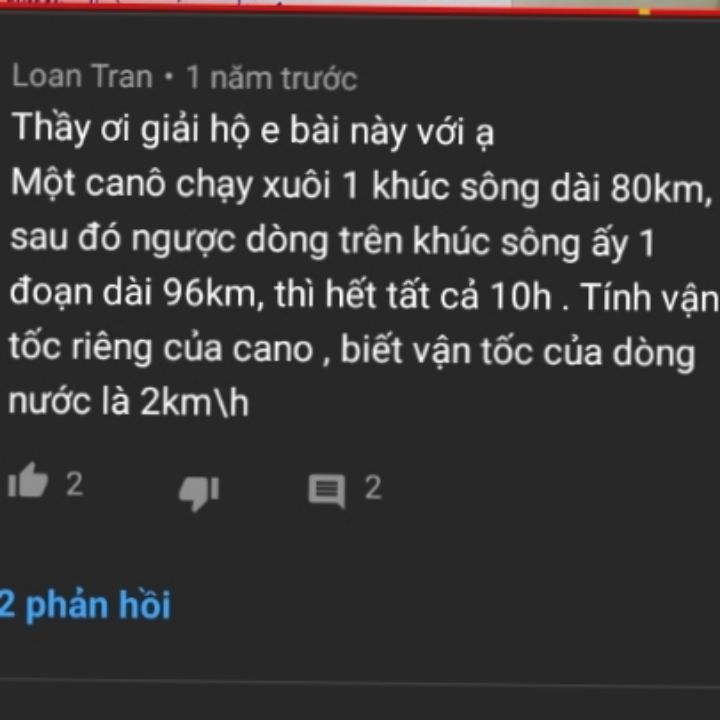 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Để chở 120 tấn hàng một đội xe dự định dùng một số xe cùng loại lúc sắp khởi hành đội được bổ sung thêm 5 xe cùng loại xe của họ vì vậy so với dự định mỗi xe phải chở ít hơn 2 tấn hỏi lúc đội có bao nhiêu xeTheo dõi (0) 2 Trả lời
Để chở 120 tấn hàng một đội xe dự định dùng một số xe cùng loại lúc sắp khởi hành đội được bổ sung thêm 5 xe cùng loại xe của họ vì vậy so với dự định mỗi xe phải chở ít hơn 2 tấn hỏi lúc đội có bao nhiêu xeTheo dõi (0) 2 Trả lời -


Tính số dụng cụ mỗi đội được giao biết 2 đội được giao tổng cộng 300 dụng cụ trong 1 tháng
bởi Nguyễn Minh Nguyệt
 31/05/2019
giúp em giải bài này
31/05/2019
giúp em giải bài này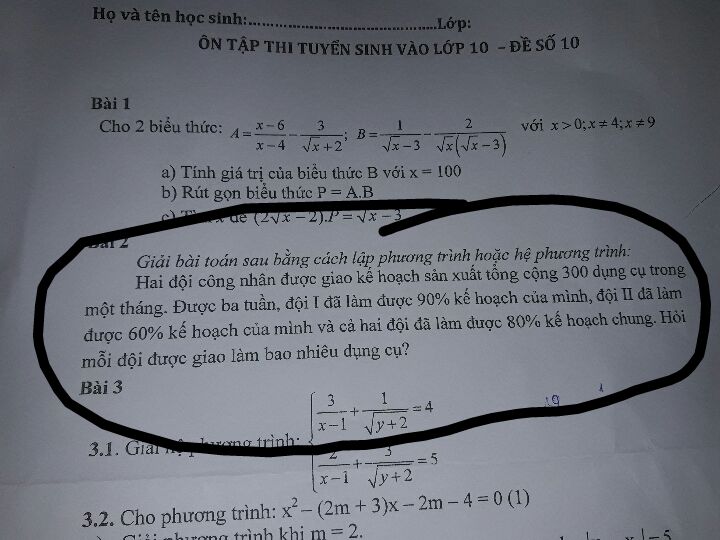 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính số học sinh lớp 9A và 9B biết 9A và 9B ủng hộ thư viện 738 quyển sách gồm hai loại sách
bởi Hoàng Thị Hương Giang
 18/05/2019
18/05/2019
Để chuẩn bị vào năm học mới học sinh lớp 9A và 9B ủng hộ thư viện 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo . Trong đó mỗi học sinh lớp 9A ủng hộ 6 quyện sách giáo khoa , 3 quyển sách tham khảo ,mỗi học sinh lớp 9B ủng hộ 5 quyển sách giáo khoa , 4 quyển sách tham khảo . Biết số sách giáo khoa ủng hộ nhiều hơn số sách tham khảo là 166 quyển . Tính số học sinh lớp 9A và 9B?
( đáp án 9A: 44 học sinh / 9B : 40 học sinh )
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 56 trang 61 SBT Toán 9 Tập 2
Bài tập 57 trang 61 SBT Toán 9 Tập 2
Bài tập 59 trang 61 SBT Toán 9 Tập 2
Bài tập 60 trang 62 SBT Toán 9 Tập 2
Bài tập 61 trang 62 SBT Toán 9 Tập 2
Bài tập 62 trang 62 SBT Toán 9 Tập 2
Bài tập 63 trang 62 SBT Toán 9 Tập 2
Bài tập 64 trang 62 SBT Toán 9 Tập 2





