Giải bài 63 tr 62 sách BT Toán lớp 9 Tập 2
Cho tam giác \(ABC\) vuông cân có \(AB = AC = 12cm\). Điểm \(M \) chạy trên \(AB\). Tứ giác \(MNCP\) là một hình bình hành có đỉnh \(N \) thuộc cạnh \(AC \) (h.6). Hỏi khi \(M \) cách \(A \) bao nhiêu thì diện tích của hình bình hành bằng \(32cm^2\) ?
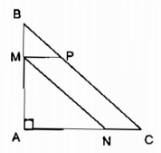
Hướng dẫn giải chi tiết
Hướng dẫn giải
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải chi tiết
Gọi độ dài đoạn \(MA = x (cm)\); điều kiện \( 0 < x < 12\)
Vì \(∆ ABC\) vuông cân tại \(A\) nên tam giác \(BMP \) vuông cân tại \(M\)
\(⇒ MP = MB = AB – AM = 12 – x (cm)\)
Diện tích hình bình hành \(MNCP\) bằng \(MP.MA\)
Suy ra: \(MP.MA = (12 – x)x\)
Ta có phương trình:
\(\eqalign{
& \left( {12 - x} \right)x = 32 \cr
& \Rightarrow {x^2} - 12x + 32 = 0 \cr
& \Delta ' = {\left( { - 6} \right)^2} - 1.32 = 36 - 32 = 4 > 0 \cr
& \sqrt {\Delta '} = \sqrt 4 = 2 \cr
& {x_1} = {{6 + 2} \over 1} = 8 \cr
& {x_2} = {{6 - 2} \over 1} = 4 \cr} \)
Cả hai giá trị \(x_1 = 8\) và \(x_2 = 4 \) thỏa mãn điều kiện bài toán
Vậy điểm \(M\) cách điểm \(A\) là \(8cm\) hoặc \(4cm\) thì diện tích hình bình hành \(MNCP\) bằng \(32cm^2.\)
-- Mod Toán 9 HỌC247
-


Nếu chảy riêng thì sau bao lâu sẽ đầy bình biết 2 vòi cùng chảy sau 4h48p thì đầy?
bởi Đức Mạnh
 01/02/2018
01/02/2018
hai vòi nước cùng chảy vào một bể thì sau 4h48p thì đầy nc . Biết mỗi giờ lượng nước ở vòi 1 chảy bằng 3/2 của lượng nước vòi 2 chảy đc.hỏi nếu chảy riêng thì sau bao lâu sễ đầy bình???
Theo dõi (1) 1 Trả lời





