Phần hướng dẫn giải bài tập Hình học 8 Bài 12 Hình vuông sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Hình học 8 Tập 1
-
Bài tập 79 trang 108 SGK Toán 8 Tập 1
a) Một hình vuông có cạnh bằng \(3cm\). Đường chéo của hình vuông đó bằng \(6cm\), \(\sqrt{18}cm\), \(5cm\) hay \(4cm\) ?
b) Đường chéo của một hình vuông bằng \(2dm\). Cạnh của hình vuông đó bằng: \(1dm, \dfrac{3}{2}dm\), \(\sqrt{2}dm\) hay \(\dfrac{4}{3}dm\) ?
-
Bài tập 80 trang 108 SGK Toán 8 Tập 1
Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.
-
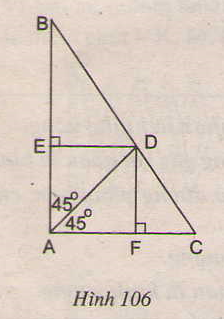
Bài tập 81 trang 108 SGK Toán 8 Tập 1
Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?
-
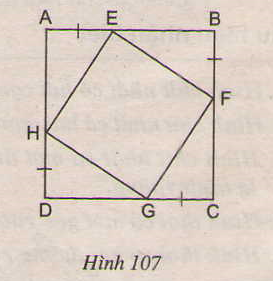
Bài tập 82 trang 108 SGK Toán 8 Tập 1
Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.
-
Bài tập 83 trang 109 SGK Toán 8 Tập 1
Các câu sau đúng hay sai ?
a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.
b) Tứ giác có hai đường chéo vuông góc nhau tại trung điểm của mỗi đường là hình thoi.
c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.
d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
-
Bài tập 84 trang 109 SGK Toán 8 Tập 1
Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.
a) Tứ giác AEDF là hình gi ? Vì sao ?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi ?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?
-
Bài tập 85 trang 109 SGK Toán 8 Tập 1
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác EMFN là hình gì? Vì sao?
-
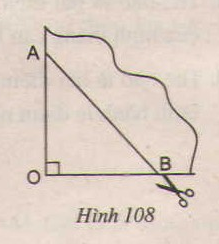
Bài tập 86 trang 109 SGK Toán 8 Tập 1
Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì ? Vì sao ? Nếu ta có OA = OB thì tứ giác nhận được là hình gì ?
-
Bài tập 144 trang 98 SBT Toán 8 Tập 1
Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N theo thứ tự là chân các đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
-
Bài tập 145 trang 98 SBT Toán 8 Tập 1
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì ? Vì sao ?
-
Bài tập 146 trang 98 SBT Toán 8 Tập 1
Cho tam giác ABC, điểm I nằm giữa B và C.
Qua I vẽ đường thẳng song song với AB, cắt AC ở H.
Qua I vẽ đường thẳng song song với AC, cắt AB ở K.
a. Tứ giác AHIK là hình gì ?
b. Điểm I nằm ở vị trí nào trên cạnh BC thì tứ giác AHIK là hình thoi ?
c. Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật ?
-
Bài tập 147 trang 98 SBT Toán 8 Tập 1
Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
-
Bài tập 148 trang 98 SBT Toán 8 Tập 1
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự ở E và F. Tứ giác EFGH là hình gì ? Vì sao ?
-
Bài tập 149 trang 98 SBT Toán 8 Tập 1
Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF.
-
Bài tập 150 trang 98 SBT Toán 8 Tập 1
Cho một hình chữ nhật có hai cạnh kề không bằng nhau. Chứng minh rằng các tia phân giác của các góc hình chữ nhật đó cắt nhau tạo thành một hình vuông.
-
Bài tập 151 trang 98 SBT Toán 8 Tập 1
Cho hình vuông ABCD. Gọi E là một điểm nằm giữa C và D. Tia phân giác của góc DAE cắt CD ở F. Kẻ FH ⊥ AE (H ∈ AE), FH cắt BC ở G.
Tính số đo góc FAG.
-
Bài tập 152 trang 99 SBT Toán 8 Tập 1
Cho hình vuông DEBC. Trên cạnh CD lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối tia ED lấy điểm M sao cho CA = DK = EM. Vẽ hình vuông DKIH (H thuộc cạnh DE). Chứng minh rằng ABMI là hình vuông.
-
Bài tập 153 trang 99 SBT Toán 8 Tập 1
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.
a. Chứng minh rằng EC = BH, EC ⊥ BH.
b. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì ? Vì sao ?
-
Bài tập 154 trang 99 SBT Toán 8 Tập 1
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK + CE = BE.
-
Bài tập 155 trang 99 SBT Toán 8 Tập 1
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC.
a. Chứng minh rằng CE vuông góc với DF
b. Gọi M là giao điểm của CE và DF. Chứng minh rằng AM = AD
HD . Gọi K là trung điểm của CD. Chứng minh rằng KA // CE.
-
Bài tập 156 trang 99 SBT Toán 8 Tập 1
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho\(\widehat {FAD} = \widehat {FDA} = {15^0}\).
a. Vẽ điểm F trong hình vuông sao cho\(\widehat {FAD} = \widehat {FDA} = {15^0}\). Chứng minh rằng tam giác DEF là tam giác đều.
b. Chứng minh rằng tam giác ABE là tam giác đều.
-
Bài tập 12.1 trang 99 SBT Toán 8 Tập 1
Hình vuông có chu vi bằng 8 thì đường chéo bằng :
A. 2
B. \(\sqrt {32} \)
C. \(\sqrt 8 \)
D. \(\sqrt 2 \)
-
Bài tập 12.2 trang 99 SBT Toán 8 Tập 1
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?
-
Bài tập 12.3 trang 99 SBT Toán 8 Tập 1
Cho hình vuông ABCD. Trên cạnh DC lấy điểm E, trên cạnh BC lấy điểm F sao cho DE = CF. Chứng minh rằng AE = DF và AE ⊥ DF.






