Bài tập 85 trang 109 SGK Toán 8 Tập 1

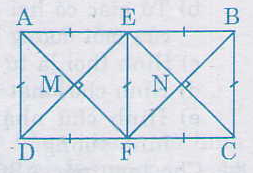
Câu a:

Tứ giác ADFE là hình vuông.

Giải thích:

Tứ giác ADFE có AE // DF, AE = DF nên là hình bình hành.

Hình bình hành ADFE có \(\widehat{M} = 90^0\) nên là hình chữ nhật.

Hình chữ nhật ADFE có AE = AD nên là hình vuông.

Câu b:

Tứ giác EMFN là hình vuông.

Giải thích:

Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành.

Do đó DE // BF

Tương tự AF // EC

Suy ra EMFN là hình bình hành.

Theo câu a, ADFE là hình vuông nên ME = MF, ME  ⊥ MF.

Hình bình hành EMFN có \(\widehat{M} = 90^0\) nên là hình chữ nhật, lại có ME = MF nên là hình vuông.

-- Mod Toán 8 HỌC247