Giải bài 149 tr 98 sách BT Toán lớp 8 Tập 1
Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Vận dụng kiến thức về các trường hợp bằng nhau của tam giác.
- Áp dụng định lí: Tổng ba góc trong một tam giác bằng \(180^0\)
Lời giải chi tiết
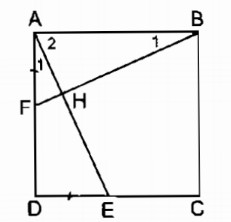
Xét ∆ ABF và ∆ DAE:
AB = DA (gt)
\(\widehat {BAF} = \widehat {ADE} = {90^0}\)
AF = DE (gt)
Do đó: ∆ ABF = ∆ DAE (c.g.c)
⇒ BF = AE
\({\widehat B_1} = {\widehat A_1}\)
Gọi H là giao điểm của AE và BF.
\(\widehat {BAF} = {\widehat A_1} + {\widehat A_2} = {90^0}\)
Suy ra: \({\widehat B_1} + {\widehat A_2} = {90^0}\)
Trong ∆ ABH ta có:
\(\widehat {AHB} + {\widehat B_1} + {\widehat A_2} = {180^0}\)
\(\widehat {AHB} = {180^0} - \left( {{{\widehat B}_1} + {{\widehat A}_2}} \right) = {180^0} - {90^0} = {90^0}\)
Vậy AE ⊥ BF.
-- Mod Toán 8 HỌC247
-


Chứng minh tam giác ABE là tam giác đều biết hình vuông ABCD có E nằm trong hình vuông và tam giác ECD cân
bởi Phong Vu
 31/05/2019
31/05/2019
Cho hình vuông ABCD, điểm E nằm trong hình vuông sao cho tam giác ECD cân có góc đáy bằng 15o.
CMR: tam giác ABE là tam giác đều
Theo dõi (0) 1 Trả lời -


Chứng minh AMIN là hình vuông biết ABC vuông tại A
bởi hoàng duy
 31/05/2019
31/05/2019
cho tam giác ABC vuông góc tại A.Đường phân giác  cắt BC tại I , từ I kẻ IM,IN lần lượt vuông góc với AB,AC.Chứng minh tứ giác AMIN là hình vuông
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A . Gọi E,G,F là trung điểm của AB,BC,AC. Từ E kẻ đường song song với BF, đường thẳng này cắt GF tại I
a. Tứ giác AEGF là hình gì ?
b. Chứng minh tứ giác BEIF là hình bình hành
c. Chứng minh tứ giác AGCI là hình thoi
d. Tìm điều kiện của tam giác ABC để tứ giác AGCI là hình vuông
mong mọi người giúp đỡ giải bài này dùm mình , cám ơn ạ
Theo dõi (0) 1 Trả lời -


Cho tam giác nhọn ABC. Vẽ ra phía ngoài của tam giác hai hình vuông ABDE và ACFH. Gọi I và K lần lượt là tâm của ha hình vuông nói trên, M là trung điểm cạnh BC
a) Chứng minh EC = BH và EC vuông góc với BH
b) Gọi N là trung điểm của EH. Tứ giác MINK là hình gì? Ví sao?
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 147 trang 98 SBT Toán 8 Tập 1
Bài tập 148 trang 98 SBT Toán 8 Tập 1
Bài tập 150 trang 98 SBT Toán 8 Tập 1
Bài tập 151 trang 98 SBT Toán 8 Tập 1
Bài tập 152 trang 99 SBT Toán 8 Tập 1
Bài tập 153 trang 99 SBT Toán 8 Tập 1
Bài tập 154 trang 99 SBT Toán 8 Tập 1
Bài tập 155 trang 99 SBT Toán 8 Tập 1
Bài tập 156 trang 99 SBT Toán 8 Tập 1
Bài tập 12.1 trang 99 SBT Toán 8 Tập 1





