Bài tập 148 trang 98 SBT Toán 8 Tập 1

Hướng dẫn giải

Vận dụng kiến thức 

- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.

- Hình bình hành có một góc vuông là hình chữ nhật.

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Lời giải chi tiết

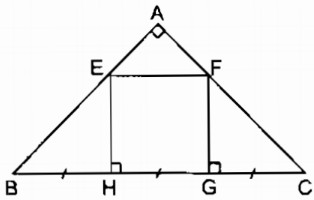
∆ ABC vuông cân tại A. \( \Rightarrow \widehat B = \widehat C = {45^0}\)

∆ BHE vuông tại H có \(\widehat B = {45^0}\)

⇒ ∆ BHE vuông cân tại H nên HB = HE

∆ CGF vuông cân tại G có \(\widehat C = {45^0}\)

⇒ ∆ CGF vuông cân tại G nên GC = GF

Ta có: BH = HG = GC (gt)

Suy ra: HE = HG = GF

EH // GF (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)

nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau)

có \(\widehat {EHG} = {90^0}\) do đó HEFG là hình chữ nhật

EH = HG (chứng minh trên)

Vậy HEFG là hình vuông.

-- Mod Toán 8 HỌC247