Bài tập 71 trang 103 SGK Toán 8 Tập 1

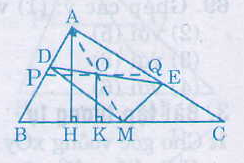
Câu a:

Tứ giác ADME có\(\widehat{A}=\widehat{D}=\widehat{E}=90^0\)

nên ADME là hình chữ nhật

O là trung điểm của đường chéo AM.

Vậy A, O, M thẳng hàng

Câu b:

Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:

Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.

Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.

-- Mod Toán 8 HỌC247