Giải bài 10.2 tr 96 sách BT Toán lớp 8 Tập 1
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Tập hợp các điểm cách đều cách đều hai cạnh của một góc là tia phân giác của góc ấy.
Lời giải chi tiết
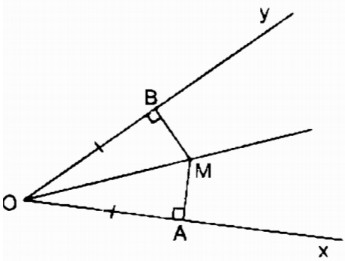
Xét hai tam giác vuông MOA và MOB: \(\widehat {MAO} = \widehat {MBO} = {90^0}\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \widehat {AOM} = \widehat {BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat {AOM} = \widehat {BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





