Giải bài 67 tr 102 sách GK Toán 8 Tập 1
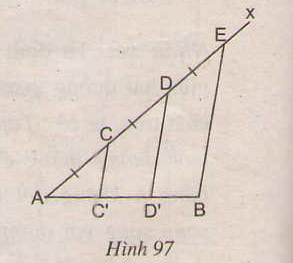
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
Hướng dẫn giải chi tiết
Ta có: EB // DD' // CC' và AE = CD = DE.
Nên theo định lí về các đường thẳng song song cách đều ta suy ra
AC' = C'D' = D'B
Vậy đoạn thẳng AB bị chia ra ba phần bằng nhau.
-- Mod Toán 8 HỌC247
-
Cho tam giác ABC có đường trung tuyến AM. Trên tia đối của tia AC lấy điểm H. Gọi I là giao điểm của BH và MA. Gọi K là giao điểm của BA và CI. Chứng minh rằng: KH song song với BC.
bởi Nguyễn Hoàng Bách Bách
17/02/2021
Cho tam giác ABC có đường trung tuyến AM. Trên tia đối của tia AC lấy điểm H. Gọi I là giao điểm của BH và MA. Gọi K là giao điểm của BA và CI. CMR: KH song song với BC
Theo dõi (0) 0 Trả lời -
Chứng minh tứ giác BPQC là hình chữ nhât?
bởi Thư Bùi
16/04/2020
Theo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 68 trang 102 SGK Toán 8 Tập 1
Bài tập 69 trang 103 SGK Toán 8 Tập 1
Bài tập 70 trang 103 SGK Toán 8 Tập 1
Bài tập 71 trang 103 SGK Toán 8 Tập 1
Bài tập 72 trang 103 SGK Toán 8 Tập 1
Bài tập 124 trang 95 SBT Toán 8 Tập 1
Bài tập 125 trang 95 SBT Toán 8 Tập 1
Bài tập 126 trang 96 SBT Toán 8 Tập 1
Bài tập 127 trang 96 SBT Toán 8 Tập 1
Bài tập 128 trang 96 SBT Toán 8 Tập 1
Bài tập 129 trang 96 SBT Toán 8 Tập 1
Bài tập 130 trang 96 SBT Toán 8 Tập 1
Bài tập 131 trang 96 SBT Toán 8 Tập 1
Bài tập 10.1 trang 96 SBT Toán 8 Tập 1
