Giải bài 61 tr 87 sách BT Toán lớp 8 Tập 1
Cho tam giác nhọn \(ABC\) có \(\widehat A = {60^0}\), trực tâm \(H.\) Gọi \(M\) là điểm đối xứng với \(H\) qua \(BC.\)
\(a)\) Chứng minh \(∆ BHC = ∆ BMC.\)
\(b)\) Tính \(\widehat {BMC}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Tổng bốn góc của một tứ giác bằng \(360^o.\)
Lời giải chi tiết
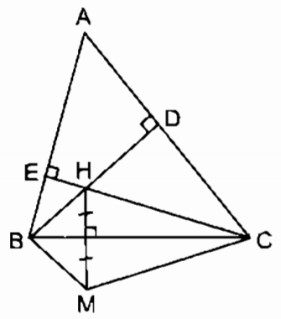
\(a)\) Vì \(M\) đối xứng với \(H\) qua trục \(BC\)
\(⇒ BC\) là đường trung trực của \(HM\)
\(⇒ BH = BM\) ( tính chất đường trung trực)
\(CH = CM\) ( tính chất đường trung trực)
+ Xét tam giác \(BHC\) và tam giác \(BMC\) có:
Cạnh \(BC\) chung
\(BH= BM\) ( chứng minh trên)
\(CH = CM\) (chứng minh trên)
Suy ra: \(∆ BHC = ∆ BMC \;\; (c.c.c)\)
\(b)\) Gọi giao điểm \(BH\) với \(AC\) là \(D,\) giao điểm của \(CH\) và \(AB\) là \(E\)
\(H\) là trực tâm của \(∆ ABC\)
\(⇒ BD ⊥ AC, CE ⊥ AB\)
Xét tứ giác \(ADHE\) ta có:
\(\widehat {DHE} +\widehat A + \widehat D + \widehat E= {360^0} \) (tổng 4 góc trong tứ giác bằng \(360^0)\)
\(\Rightarrow \widehat {DHE} = {360^0} - \left( {\widehat A + \widehat D + \widehat E} \right) \)
\(= {360^0} - \left( {{{60}^0} + {{90}^0} + {{90}^0}} \right) = {120^0}\)
\(\widehat {BHC} = \widehat {DHE}\) (đối đỉnh)
\(∆ BHC = ∆ BMC\) (chứng minh trên)
\( \Rightarrow \widehat {BMC} = \widehat {BHC}\)
Suy ra: \(\widehat {BMC} = \widehat {DHE} = {120^0}\)
-- Mod Toán 8 HỌC247
-


2.Vẽ tam giác ABC
a)Tìm điểm M là đối xứng của điểm C qua đường thẳng AB
b)Hai tam giác ABC và ABM có bằng nhau không ?Vì sao?
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác BGC = tam giác BMC biết G là trọng tâm của tam giác ABC
bởi Dương Minh Tuấn
 31/08/2019
31/08/2019
Cho tam giác ABC đều trọng tâm G.Gọi M là điểm đối xứng với G qua BC a) Chứng minh : tam giác BGC = tam giác BMC b) TÍnh các góc của tam giác BMC
Theo dõi (0) 1 Trả lời -


Chứng minh HA là tia phân giác của góc MHN biết D và E là các điểm đối xứng với H qua AB và AC
bởi Mai Trang
 31/08/2019
31/08/2019
Cho \(\Delta ABC\) \(\left(\widehat{A}< 90\right)\), kẻ đường cao AH. Gọi D và E lần lượt là các điểm đối xứng với H qua AB và AC . Đoạn thẳng ED cắt AB và AC theo thứ tự ở M và N. C/minh:
\(a,AD=AE\)
b, HA là tia phân giác của góc MHN
c, CM // HD
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 42 trang 89 SGK Toán 8 Tập 1
Bài tập 60 trang 86 SBT Toán 8 Tập 1
Bài tập 62 trang 87 SBT Toán 8 Tập 1
Bài tập 63 trang 87 SBT Toán 8 Tập 1
Bài tập 64 trang 87 SBT Toán 8 Tập 1
Bài tập 65 trang 87 SBT Toán 8 Tập 1
Bài tập 66 trang 87 SBT Toán 8 Tập 1
Bài tập 67 trang 87 SBT Toán 8 Tập 1
Bài tập 68 trang 87 SBT Toán 8 Tập 1
Bài tập 69 trang 88 SBT Toán 8 Tập 1
Bài tập 70 trang 88 SBT Toán 8 Tập 1
Bài tập 71 trang 88 SBT Toán 8 Tập 1
Bài tập 72 trang 88 SBT Toán 8 Tập 1





