Bài tập 71 trang 88 SBT Toán 8 Tập 1

Hướng dẫn giải

+) Trong hình thang cân, hai cạnh bên bằng nhau.

+) Trong hình thang cân, hai đường chéo bằng nhau.

+) Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

Lời giải chi tiết

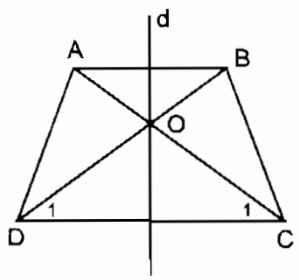
Hình thang cân \(ABCD\) có \(AB // CD.\) Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD.\)

Xét \(∆ ADC\) và \(∆ BCD:\)

\(AD = BC\) ( tính chất hình thang cân)

\(AC = BD\) ( tính chất hình thang cân)

\(CD\) cạnh chung

Do đó \(∆ ADC = ∆ BCD \;\;(c.c.c)\)

\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)  

\(⇒ ∆ OCD\) cân tại \(O\)

\(⇒ OC = OD\) nên \(O\) nằm trên đường trung trực của \(CD.\)

Trục đối xứng của hình thang cân là đường thẳng trung trực của hai đáy.

Vậy \(O\) thuộc trục đối xứng của hình thang cân

-- Mod Toán 8 HỌC247