Bài tập 117 trang 94 SBT Toán 8 Tập 1

Lý thuyết5 Trắc nghiệm

30 BT SGK

179 FAQ

Giải bài 117 tr 94 sách BT Toán lớp 8 Tập 1

Chứng minh rằng ba điểm C, B, D trên hình 18 thẳng hàng.

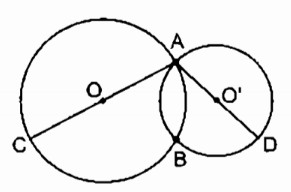
Hình học 8 Bài 9 Trắc nghiệm Hình học 8 Bài 9 Giải bài tập Hình học 8 Bài 9

Hướng dẫn giải chi tiết

Hướng dẫn giải

Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.

Lời giải chi tiết

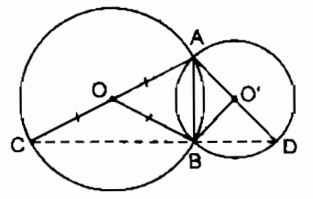
Nối AB, BO, BC, BO’, BD.

Trong ∆ ABC ta có:

OA = OC = R (bán kính đường tròn (O))

nên BO là đường trung tuyến của ∆ ABC

mà BO = R(bán kính (O))

⇒ BO = OA = OC = \({1 \over 2}\)AC

nên tam giác ABC vuông tại B \( \Rightarrow \widehat {ABC} = {90^0}\)

Trong ∆ ABD ta có: AO’ = O’D = R’ (bán kính (O’))

nên BO’ là đường trung tuyến của ∆ ABD

mà BO’ = R’ (bán kính (O’)) ⇒ BO’ = AO’ = O’D = \({1 \over 2}\)AD

nên tam giác ABD vuông tại B \( \Rightarrow \widehat {ABD} = {90^0}\)

\(\widehat {ABC} + \widehat {ABD} = \widehat {CBD}\)

\( \Rightarrow \widehat {CBD} = {90^0} + {90^0} = {180^0}\)

Vậy C, B, D thẳng hàng.

-- Mod Toán 8 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 117 trang 94 SBT Toán 8 Tập 1 HAY thì click chia sẻ

YOMEDIA

Tìm trong hình vẽ những cặp góc nhọn bằng nhau

bởi can chu 06/04/2019

cho tam giác ABC vuông góc ở đỉnh A.Vẽ AH vuông góc với BC, HE vuông góc với AC, HF vuông góc với AB ( H thuộc BC; E thuộc AC; F thuộc AB).Tìm trong hình vẽ những cặp góc nhọn bằng nhau, Biết rằng 2 góc có 2 cặp cạnh tương ứng vuông góc thì bằng nhau

Theo dõi (0) 1 Trả lời
Chứng minh tứ giác MBCN là hình bình hành

bởi Anh Trần 31/05/2019

Cho hình bình hành ABCD có AB=2CD và góc D=60⁰ .Gọi M ,N theo thứu tự là trung điểm cảu AB và CD

a,Chứng minh tứ giác MBCN là hình bình hành và MC⊥BN

c, Tính số đo góc DMC

Theo dõi (0) 1 Trả lời
Chứng minh ABEC là hình bình hành biết M là trung điểm của BC, AM cắt DC tại E

bởi Nguyễn Ngọc Sơn 31/05/2019

cho hcn ABCD ,M là trung điểm của BC, AM cắt DC tại E

a, chứng minh ABEC là hình bình hành

b, Qua D vẽ đường thẳng song song với AC ,đường này cắt BC tại F .Chứng minh BEFD là hình thoi.

c ,Gọi I là giao điểm của AC và BD ,K là trung điểm của È. Chứng minh C là trung điểm của IK.

Theo dõi (0) 1 Trả lời
Chứng minh hình chữ nhật là hình thang cân

bởi Phan Thiện Hải 25/04/2019

Chứng minh hình chữ nhật là hình thang cân

Theo dõi (0) 1 Trả lời
Chứng minh tứ giác MNPH là hình thang cân

bởi Trần Phương Khanh 31/05/2019

Cho tam giác ABC (AB<AC) đường cao AH. Gọi M, N, P lần lượt là trung điểm của cạnh BC, CA, AB. Chứng minh rằng:

a) NP là đường trung trực của AH

b) Tứ giác MNPH là hình thang cân

Theo dõi (0) 1 Trả lời
Tính GTBT A = -x^2 + 4x + 3

bởi Nguyễn Minh Minh 31/05/2019

Bài 1: Cho ΔDEF, I là trung điểm của EF. Trên tia đối của tia ID lấy điểm K sao cho ID = IK.

a. Tứ giác DEKF là hình gì? Vì sao?

b. Tìm điều kiện của ΔDEF để tứ giác DEKF là hình chữ nhật?

Bài 2: Tính giá trị của biểu thức sau:

A = -x² + 4x + 3

Theo dõi (0) 1 Trả lời