Bài tập 122 trang 95 SBT Toán 8 Tập 1

Hướng dẫn giải

Hình tứ giác có ba góc vuông là hình chữ nhật

Hình chữ nhật có hai đường chéo bằng nhau.

Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy

Lời giải chi tiết

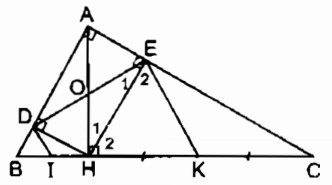
a. Xét tứ giác ADHE:

\(\widehat A = {90^0}\) (gt)

\(\widehat {ADH} = {90^0}\) (vì HD ⊥ AB)

\(\widehat {AEH} = {90^0}\) (vì HE ⊥ AC)

Suy ra tứ giác ADHE là hình chữ nhật (vì có ba góc vuông)

⇒ AH = DE (tính chất hình chữ nhật)

b. ∆ BHD vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH

⇒ DI = IB = \({1 \over 2}\) BH (tính chất tam giác vuông)

⇒ ∆ IDB cân tại I \( \Rightarrow \widehat {DIB} = {{{{180}^0} - \widehat B} \over 2}\) (1)

∆ HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC

⇒ EK = KH = \({1 \over 2}\)HC (tính chất tam giác vuông)

⇒ ∆ KHE cân tại K \( \Rightarrow \widehat {EKH} = {{{{180}^0} - \widehat {KHE}} \over 2}\) (2)

Tứ giác ADHE là hình chữ nhật

⇒ HE // AD hay HE // AB

 ⇒ \(\widehat B = \widehat {KHE}\) (đồng vị) (3)

Từ (1), (2) và (3) suy ra: \(\widehat {DIB} = \widehat {EKH}\)

⇒ DI // EK (vì có cặp góc đồng vị bằng nhau).

-- Mod Toán 8 HỌC247