Bài tập 116 trang 94 SBT Toán 8 Tập 1

Hướng dẫn giải

Tính chất hình chữ nhật: Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Định lý Py - ta - go trong tam giác ABC vuông tại A: \(AB^2+AC^2=BC^2\)

Lời giải chi tiết

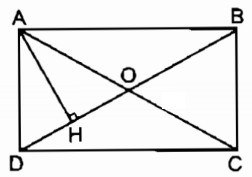
Ta có: DB = HD + HB = 2 + 6 = 8(cm)

AC = DB (tính chất hình chữ nhật)

OA = OB = OC = OD = \({1 \over 2}\)BD = 4(cm)

OD = OH + HD

⇒ OH = OD – HD = 4 – 2 = 2(cm)

AH ⊥ OD có HO = HD = 2(cm)

Suy ra: ∆ ADO cân tại A

⇒ AD = AO = 4(cm)

Trong tam giác vuông ABD có \(\widehat {BAD} = {90^0}\)

\(B{D^2} = A{B^2} + A{D^2}\) (định lý Pi-ta-go) \( \Rightarrow A{B^2} = B{D^2} - A{D^2}\)

\(AB = \sqrt {B{D^2} - A{D^2}}  = \sqrt {{8^2} - {4^2}}  = \sqrt {48}  \approx 7\) (cm).

-- Mod Toán 8 HỌC247