Giải bài 120 tr 95 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng tính chất đường trung bình của tam giác
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến tuyến ứng với cạnh huyền bằng nửa cạnh ấy
Định nghĩa hình thang cân: Hình thang có hai góc ở đáy bằng nhau là hình thang cân.
Lời giải chi tiết
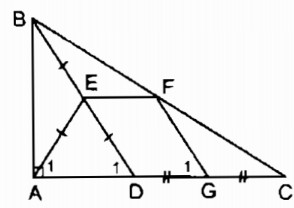
Trong ∆ BDC ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của ∆ BDC
⇒ EF // DC
hay EF // AG
Suy ra: Tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD ⇒ \({\widehat G_1} = {\widehat D_1}\) (đồng vị) (1)
Trong tam giác ABD vuông tại A có AE là trung tuyến thuộc cạnh huyền BD
⇒ AE = ED = \({1 \over 2}\)BD (tính chất tam giác vuông)
nên ∆ AED cân tại E \( \Rightarrow {\widehat A_1} = {\widehat D_1}\) (2)
Từ (1) và (2) suy ra: \({\widehat A_1} = {\widehat G_1}\)
Vậy hình thang AEFG là hình thang cân (theo định nghĩa).
-- Mod Toán 8 HỌC247
-


1. cho tam giác ABC,góc A=90 độ,FB=FC.Từ F keFM ⊥ A,FN⊥ AB (M ∈ AC)(N ∈ AB)
a) tứ giác AMFN là hình gì ? vì sao ?
b) gọi K là điểm đối xứng với F qua AB tứ giác AFBK là hình gì ? vì sao ?
c) biết AB=5,AC=6 tính SAABC= ?
Theo dõi (0) 1 Trả lời -


Chứng minh AHFK là hình chữ nhật
bởi Ngoc Nga
 31/05/2019
31/05/2019
cho hình chữ nhật abcd. Nối C với điểm E trên BD. Trên tia đối của EC, lấy F sao cho E trung điểm CF. Vẽ FH vuông góc AB, FK vuông góc AD. Chứng minh
a) AHFK là hình chữ nhật
b) AF//BD, HK//AC
c) E, H, K thẳng hàng
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi F,K lần lượt là trung điểm của GB và GC
a) Tứ giác DEFK là hình gì
b) tam giác ABC có thêm điều kiện gì, thì DEFK là hình chữ nhật
Theo dõi (0) 1 Trả lời -


Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 3m và nếu mỗi chiều giảm đi 2m thì diện tích giảm 50m vuông tính diện tích hình chữ nhật đó.
Giúp mình với!!!
Theo dõi (0) 1 Trả lời -


Chứng minh các dấu hiệu của hình chữ nhật
bởi hà trang
 31/05/2019
31/05/2019
Chứng minh các dấu hiệu của hình chữ nhật:
a)Tứ giác có ba góc vuông là hình chữ nhật.
b)Hình thang cân có một góc vuông là hình chữ nhật:
c)Hình bình hành có một góc vuông là hình chữ nhật.
d)Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
CẦN GẤP Ạ!!!
Theo dõi (0) 1 Trả lời -


Chứng minh NOPQ là hình bình hành với N, O, P, Q tương ứng là trung điểm của AB, BC, CD, và DA
bởi minh dương
 31/05/2019
31/05/2019
cho tứ giác ABCD. gọi N, O, P, Q tương ứng là trung điểm của AB, BC, CD, và DA
a)_ chứng minh rằng NOPQ là hình bình hành
b) nếu có thêm AC vuông góc BD, chứng minh NOPQ là hình chữ nhật
Theo dõi (0) 1 Trả lời





