Hướng dẫn Giải bài tập Toán 7 Chân trời sáng tạo Chương 8 Bài 7 Tính chất ba đường trung tuyến của tam giác giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khám phá 1 trang 73 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Vẽ tam giác ABC, xác định trung điểm D của cạnh BC và vẽ đoạn thẳng nối hai điểm A và D.
-
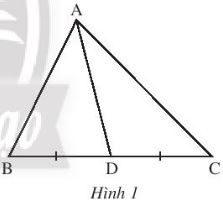
Thực hành 1 trang 73 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Em hãy viết tiếp các đường trung tuyến còn lại của tam giác ABC (Hình 1).
-
Vận dụng 1 trang 73 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
a) Vẽ đường trung tuyến DH của tam giác DEF (Hình 2).
b) Vẽ đường trung tuyến MK của tam giác MNP (Hình 3).
c) Vẽ tam giác nhọn IJK và tất cả các đường trung tuyến của nó.
-
Hoạt động khám phá 2 trang 74 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
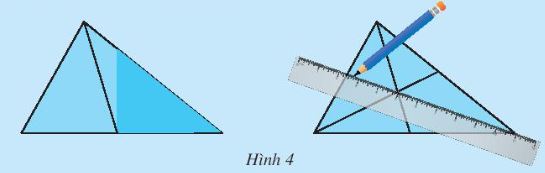
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.
Em hãy quan sát vào cho biết:
- AD có phải đường trung tuyến của tam giác ABC hay không?
- Các tỉ số \(\dfrac{{BG}}{{BE}}\), \(\dfrac{{CG}}{{CF}}\), \(\dfrac{{AG}}{{AD}}\) bằng bao nhiêu ?
-
Thực hành 2 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
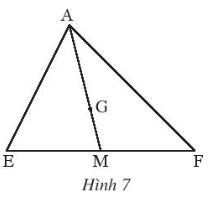
Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM.
Hãy tính các tỉ số:
a) \(\dfrac{{GM}}{{AM}}\)
b) \(\dfrac{{GM}}{{AG}}\)
c) \(\dfrac{{AG}}{{GM}}\)
-
Vận dụng 2 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm của các tam giác ABC và BCD. Chứng minh rằng AI = IJ = JD.
-
Giải bài 1 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
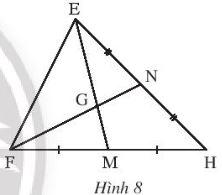
Quan sát Hình 8.
Tìm số thích hợp để ghi vào chỗ chấm trong các đẳng thức sau:
\(\begin{array}{l}EG = ...EM;\,\,\,GM = ...EM;\,\,\,\,GM = ...EG\\FG = ...GN;\,\,\,\,\,FN = ...GN;\,\,\,\,\,FN = ...FG\end{array}\)
-
Giải bài 2 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
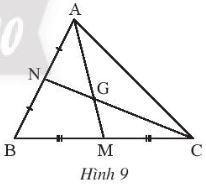
Quan sát Hình 9
a) Biết AM = 15 cm, tính AG
b) Biết GN = 6 cm, tính CN
-
Giải bài 3 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.
a) Chứng minh rằng BG song song với EC.
b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI
-
Giải bài 4 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
-
Giải bài 5 trang 76 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.
-
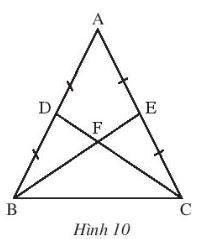
Giải bài 6 trang 76 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.
-
Giải bài 1 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh:
a) \({S_{AMB}} = {S_{AMC}}\)
b) \({S_{ABG}} = 2{S_{BMG}}\)
c) \({S_{GAB}} = {S_{GBC}} = {S_{GAC}}\)
-
Giải bài 2 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A. Chứng minh tam giác ABC là tam giác cân.
-
Giải bài 3 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có hai trung tuyến AM và CN cắt nhau tại G.
a) Biết AM = 12 cm, tính AG.
b) Biết GN = 3 cm, tính CN.
c) Tìm x biết AG = 3x – 4, GM = x.
-
Giải bài 4 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có ba trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: \(GA + GB + GC = \frac{2}{3}\left( {AM + BN + CP} \right)\)
-
Giải bài 5 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Vẽ AH vuông góc với BC tại H. Cho biêý HB = HM. Chứng minh:
a) \(\Delta ABH = \Delta AMH\)
b) \(AG = \frac{2}{3}AB\)

.JPG)