Giải bài 1 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST

Phương pháp giải

So sánh đường cao và các cạnh đáy tương ứng của các tam giác

Lời giải chi tiết

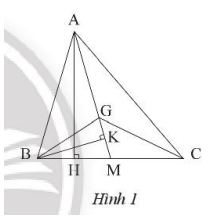
a) Vẽ đường cao AH của tam giác ABC.

Hai tam giác AMB và AMC có cùng đường cao AH và có cạnh đáy bằng nhau: BM = CM

Suy ra: \({S_{AMB}} = {S_{AMC}}\)(vì \({S_{AMB}} = \frac{1}{2}.AH.BM{;^{}}{S_{AMC}} = \frac{1}{2}.AN.CM\))

b) Vẽ đường cao BK của tam giác BGM.

Hai tam giác ABG và BMG có cùng đường cao BK và có cạnh đáy AG = 2MG.

Suy ra: \({S_{ABG}} = \frac{1}{2}.BK.AG = \frac{1}{2}.BK.2MG = 2.\frac{1}{2}.BK.MG = 2{S_{BMG}}\)

c) Ta có:

\({S_{ABG}} = \frac{2}{3}{S_{ABM}} = \frac{1}{3}{S_{ABC}}\)

Tương tự: \({S_{ACG}} = \frac{2}{3}{S_{ACM}} = \frac{1}{3}{S_{ABC}}\)

Suy ra: \({S_{BCG}} = \frac{1}{3}{S_{ABC}}\)

Vậy: \({S_{GAB}} = {S_{GBC}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\) 

-- Mod Toán 7 HỌC247