Vận dụng 2 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
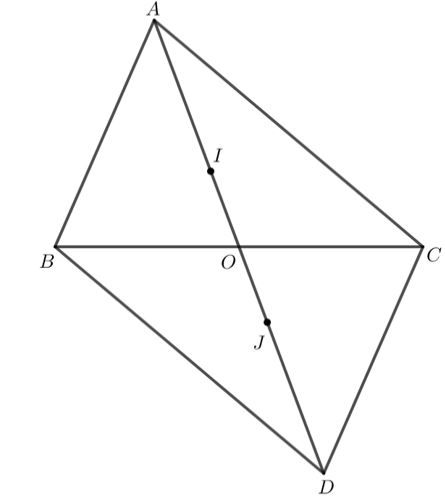
Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm của các tam giác ABC và BCD. Chứng minh rằng AI = IJ = JD.
Hướng dẫn giải chi tiết Vận dụng 2
Phương pháp giải
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy .
- Ta sẽ chứng minh AI = IJ = JD = \(\dfrac{2}{3}\)AO = \(\dfrac{2}{3}\)OD
Lời giải chi tiết
Vì I là trọng tâm tam giác ABC theo giả thiết nên ta có
\(AI = \dfrac{2}{3}AO = 2IO\)(định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
\(DJ = \dfrac{2}{3}OD = 2OJ\) (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
\( \Rightarrow AI = DJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD = 2OI = 2OJ\)
Mà OI = OJ do cùng \( = \dfrac{1}{3}OA = \dfrac{1}{3}OD\)(tính chất trọng tâm trong tam giác)
\( \Rightarrow 2OI = 2OJ = 2\dfrac{1}{3}AO = 2\dfrac{1}{3}OD = IJ\)
\( \Rightarrow AI = DJ = IJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD\)(điều phải chứng minh)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động khám phá 2 trang 74 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 75 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 76 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 76 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST