Bài tập 33 trang 91 SBT Toán 6 Tập 2
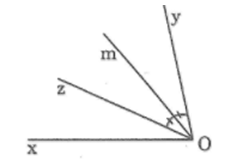
Cho hai tia Oy, Oz cùng nằm trong nửa mặt phẳng có bờ chứa tia Ox sao cho \(\widehat {xOy} = {80^0}\), \(\widehat {xOz} = {30^0}\). Gọi Om là tia phân giác của góc yOz. Tính \(\widehat {xOm}\)
Hướng dẫn giải chi tiết
Vì Oy và Oz cùng nằm trên một nửa mặt phẳng bờ chứa tia Ox, và \(\widehat {xOy} > \widehat {xOz}\)
nên tia Oz nằm giữa hai tia Ox; Oy
Suy ra:
\(\begin{array}{l}
\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\\
\Rightarrow \widehat {zOy} = \widehat {xOy} - \widehat {xOz}\\
= {80^0} - {30^0} = {50^0}
\end{array}\)
Vì Om là tia phân giác của \(\widehat {yOz}\) nên:
\(\begin{array}{l}
\widehat {zOm} = \widehat {mOy}\\
= \frac{{\widehat {yOz}}}{2} = \frac{{{{50}^0}}}{2} = {25^0}
\end{array}\)
Vì Oz nằm giữa Ox và Om: nên \(\widehat {xOm} = \widehat {xOz} + \widehat {zOm}\)
Suy ra: \(\widehat {xOm} = {30^0} + {25^0} = {55^0}\)
-- Mod Toán 6 HỌC247
-


Cho góc xOy và góc yOz là 2 góc phụ nhau( Ox và Oz nằm trên 2 nửa mặt phẳng đối nhau) Gọi Ot là tia phân giác của xOy, Om là tia phân giác của yOz. Tính góc mOt
Theo dõi (0) 1 Trả lời -


Cho AB ct CD tai O.Phan giac cua goc AOC la OM,phan giac cua goc BOD la OM.chung minh thia OM va ON la hai tia doi nhau .
Theo dõi (0) 2 Trả lời -


cho góc aOb và bOc là 2 góc kề bù. vẽ On và Om là tia phân giác lần lượt của góc aOb và bOc. vẽ Op là tia đối của tia On,so sánh góc nOb và pOc.
Theo dõi (0) 1 Trả lời -


Bài 1: Trên nửa mặt phẳng có bờ chứa tia Ox, có hai tia Oy, Oz sao cho góc xOy=60 độ, xOz= 110 độ
a) Hỏi tia Oy có phải là tia phân giác của góc xOz không? Vì sao?
b)Tính số đo góc kề bù với góc yOz
c)Vẽ tia đối Ot của tia Oy. Hỏi tia Ox có phải là tia phân giác của góc tOz không? vì sao?
Theo dõi (0) 2 Trả lời -


trên 1 nửa mặt phẳng có chứa bờ Oz vẽ hai tia Ox và Oy sao cho góc xOy = 60 độ ; góc xOZ = 120 độ
a tính số đo góc yOz
b vẽ tia Ot là tai phân giác của góc yOz. Tính góc tOz
Theo dõi (0) 1 Trả lời -


Tính góc x'Ot biết xOy, yOx' kề bù và xOy=30 độ
bởi Nguyễn Hồng Tiến
 14/11/2018
14/11/2018
1)Vẽ hai góc kề bù xOy, yOx', biết góc xOy=30°.Gọi Ot là tia phân giác của góc xOy.Tính góc x'Ot .
2) Vẽ hai góc kè bù xOy, yOx', biết xOy=100° . Gọi Ot là tia phân giác của góc xOy, Ot' là tia phân giác của góc x'Oy.Tính góc x'Ot , xOt', tOt'.
3) Vẽ góc bẹt xOy.Vẽ tia phân giác Om của góc đó. Vẽ tia phân giác Oa của xOm. Vẽ tia phân giác Ob của góc mOy. Tính số đo góc aOb.
4)Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết góc xOy=30°, xOz=80°.Vẽ tia phân giác Om của góc xOy. Vẽ tia phân giác On của góc yOz.Tính góc mOn .
Theo dõi (0) 1 Trả lời -


vẽ hình để chứng tỏ rằng những câu đây là sai
2 tia chung goc luon la 2 tia doi nhau
2 tia chung gốc luôn là 2 tia trùng nhau
Theo dõi (0) 1 Trả lời -


Bài 1: Cho 2 góc kề bù xOy và yOz. Biết góc xOy=124 độ
a) tính góc yOz?
b)kẻ phân giác Ot của góc xOy. Tính góc tOz
Bài 2: Trên cùng 1 nửa mặt bờ phẳng là đường thẳng chưa tia Ox.Vẽ 2 tia Oy, Oz sao cho góc xOy=35 độ, xOz=70 độ
a) Trong 3 tia Ox, Oy, Oz tia nằm giữa 2 tia còn lại? Vì sao?
b) Tính góc yOz
c) Chứng tỏ tia Oy là phân giác của góc xOz?
ai nhanh tay thì mình tick nha~ (Quay tay đại pháp đi)
Theo dõi (0) 1 Trả lời -


Trên nữa mặt phẳng bờ chứa tia Ox vẽ xÔz = 35 độ, xO6y = 70 độ
a. Tia nào nằm giữa 2 tia còn lại? Vì sao
b. Tính zÔy
c. Tia Oz có phải là tia phân giác của góc xÔy ko? Vì sao
d. Gọi Om là tia phân giác của góc xÔz. Tính mÔy
e. Gọi Ot là tia đối của tia Ox. Tính tÔy
Theo dõi (0) 1 Trả lời -


Trên cùng một nửa mặt phẳng bờ chứa tia ox ve hai tia oy và oz sao cho góc xôy =30độ , xôz =60độ
a, Trong ba tia ox, oy, oz tia nào nằm giữa hai tia còn lại? Vì sao?
b, Tia oy có phải là tia phân giác của góc xôz không Vì sao?
Nhớ vẽ hình ra nhé
Thanks
Theo dõi (0) 1 Trả lời -


Trong 3 tia Ox, Om, On thì tia nào nằm giữa hai tia còn lại biết xOm=120 độ và xOn=60 độ?
bởi Spider man
 13/11/2018
13/11/2018
Bài 1: Bạn Tuấn đọc hết quyển sách trong 2 ngày. Ngày đầu đọc được 3/5 tổng số trang thì còn lại 8 trang để đọc vào ngày thứ 2. Tính số trang của quyển sách?
Bài 2: hai vòi nước cùng chảy vào một bể nếu vòi 1 chảy một mình thì sau 4 giờ đầy bể, vòi 2 chảy một mình thì sau 6 giờ đầy bể. hỏi cả hai vòi cùng chảy sau 1 giờ được mấy phần của bể và sau bao lâu hai vòi chảy đầy bể
Bài 3:
A= 2/3.4 + 2/4.5 + 2/5.6 + ....+ 2/98.99B= -1/2.3.4 + -1/3.4.5 + -1/4.5.6 +....+ -1/28.29.30
Bài 4: Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox, vẽ 2 tia Om và On sao cho xÔm = 120o , xÔn = 60o.
a/ Trong 3 tia Ox,Om,On tia nào nằm giữa 2 tia còn lại? Vì sao?
b/ tính số đo góc mÔn?
c/ gọi tia Ox' là tia đối của tia Ox, Tính số đo góc x'Ôm?
d/ gọi Oy là tia phân giác của góc x'Ôm. tính số đo của góc nOy?
* Bài 4 vẽ hình hộ mh ^-^
---------- Mình đang cần gấp, giúp mình với ---------- Cảm ơn !!
Theo dõi (0) 1 Trả lời -


Cho 2 tia ox và oy vuông góc vs nhau. TRong góc xoy vẽ tia oa và ob sao cho aox=boy=30 độ.Vẽ tia oc sao cho oy là tia phân giác của aoc.Chứng minh rằng:
a, Oa là tia phân giác của box.
b, Ob vuông góc vs Oc.
các bạn nhớ vẽ hình giúp mik nha, mik c.ơn,ai giải đầy đủ có like nhé.<3
Theo dõi (0) 1 Trả lời -


Trên cùng một nửa mặt phẳng bờ là đường thẳng chứa tia ox.Vẽ hai tia oy, oz sao cho góc xoy =400, góc xoz = 1200.Vẽ om là tia phân giác góc xoy, on lả phân giác của góc xoz
a) Tính góc xom, góc xon, góc mon
b) Tia oy có là tia phân giác của góc mon ?
c) Gọi ot là tia đối của tia ox, ot' là tia đối tia oz. So sánh góc toz và xot'
Các bạn giải dùm mình bài toán này nhak.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 35 trang 87 SGK Toán 6 Tập 2
Bài tập 36 trang 87 SGK Toán 6 Tập 2
Bài tập 37 trang 87 SGK Toán 6 Tập 2
Bài tập 30 trang 90 SBT Toán 6 Tập 2
Bài tập 31 trang 91 SBT Toán 6 Tập 2
Bài tập 32 trang 91 SBT Toán 6 Tập 2
Bài tập 34 trang 91 SBT Toán 6 Tập 2
Bài tập 6.1 trang 92 SBT Toán 6 Tập 2
Bài tập 6.2 trang 92 SBT Toán 6 Tập 2
Bài tập 6.3 trang 92 SBT Toán 6 Tập 2
Bài tập 6.4 trang 92 SBT Toán 6 Tập 2
Bài tập 6.5 trang 92 SBT Toán 6 Tập 2
Bài tập 6.6 trang 92 SBT Toán 6 Tập 2
Bài tập 30 trang 87 SGK Toán 6 Tập 2
Bài tập 31 trang 87 SGK Toán 6 Tập 2
Bài tập 32 trang 87 SGK Toán 6 Tập 2