HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 7 B├Āi 27 Thß╗ā t├Łch m├┤n To├Īn hß╗Źc lß╗øp 11 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng 1 trang 61 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Khi mua m├Īy ─æiß╗üu ho├Ā, b├Īc An ─æŲ░ß╗Żc hŲ░ß╗øng dß║½n rß║▒ng mß╗Śi m├®t khß╗æi cß╗¦a ph├▓ng cß║¦n c├┤ng suß║źt ─æiß╗üu ho├Ā khoß║Żng 200 BTU. C─ān ph├▓ng b├Īc An cß║¦n lß║»p m├Īy c├│ dß║Īng h├¼nh hß╗Öp chß╗» nhß║Łt, rß╗Öng 4 m, d├Āi 5 m v├Ā cao 3 m. Hß╗Åi b├Īc An cß║¦n mua loß║Īi ─æiß╗üu ho├Ā c├│ c├┤ng suß║źt bao nhi├¬u BTU?
-
Luyß╗ćn tß║Łp 1 trang 62 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho khß╗æi ch├│p ─æß╗üu S.ABCD c├│ cß║Īnh ─æ├Īy bß║▒ng a, cß║Īnh b├¬n bß║▒ng b. T├Łnh thß╗ā t├Łch cß╗¦a khß╗æi ch├│p.
-
Luyß╗ćn tß║Łp 2 trang 62 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
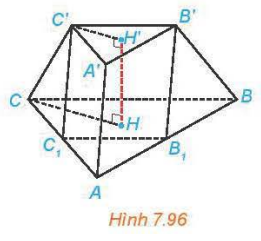
Cho khß╗æi ch├│p cß╗źt ─æß╗üu ABC.A'B'C' c├│ ─æŲ░ß╗Øng cao HH' = h, hai mß║Ęt ─æ├Īy ABC, A'B'C' c├│ cß║Īnh tŲ░ŲĪng ß╗®ng bß║▒ng 2a, a.
a) T├Łnh thß╗ā t├Łch cß╗¦a khß╗æi ch├│p cß╗źt.
b) Gß╗Źi B1,C1 tŲ░ŲĪng ß╗®ng l├Ā trung ─æiß╗ām cß╗¦a AB, AC. Chß╗®ng minh rß║▒ng AB1C1.A'B'C' l├Ā mß╗Öt h├¼nh l─āng trß╗ź. T├Łnh thß╗ā t├Łch khß╗æi l─āng trß╗ź AB1C1.A'B'C'.
-
Vß║Łn dß╗źng trang 63 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Mß╗Öt sß╗Źt ─æß╗▒ng ─æß╗ō c├│ dß║Īng h├¼nh ch├│p cß╗źt ─æß╗üu (H.7.98). ─É├Īy v├Ā miß╗ćng sß╗Źt l├Ā c├Īc h├¼nh vu├┤ng tŲ░ŲĪng ß╗®ng c├│ cß║Īnh bß║▒ng 60 cm, 30 cm, cß║Īnh b├¬n cß╗¦a sß╗Źt d├Āi 50 cm. T├Łnh thß╗ā t├Łch cß╗¦a sß╗Źt.
-
Giß║Żi B├Āi 7.28 trang 63 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho khß╗æi ch├│p ─æß╗üu S.ABC, ─æ├Īy c├│ cß║Īnh bß║▒ng a, cß║Īnh b├¬n bß║▒ng b. T├Łnh thß╗ā t├Łch cß╗¦a khß╗æi ch├│p ─æ├│. Tß╗½ ─æ├│ suy ra thß╗ā t├Łch cß╗¦a khß╗æi tß╗® diß╗ćn ─æß╗üu c├│ cß║Īnh bß║▒ng a.
-
Giß║Żi B├Āi 7.29 trang 63 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho khß╗æi l─āng trß╗ź ─æß╗®ng ABC.A'B'C' c├│ AA'= 5 cm, AB = 6 cm, BC = 2 cm, \(\widehat{ABC} = 150 \circ\). T├Łnh thß╗ā t├Łch cß╗¦a khß╗æi l─āng trß╗ź.
-
Giß║Żi B├Āi 7.30 trang 63 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho khß╗æi ch├│p ─æß╗üu S.ABCD, ─æ├Īy c├│ cß║Īnh 6 cm. T├Łnh thß╗ā t├Łch cß╗¦a khß╗æi ch├│p ─æ├│ trong c├Īc trŲ░ß╗Øng hß╗Żp sau.
a) Cß║Īnh b├¬n tß║Īo vß╗øi mß║Ęt ─æ├Īy mß╗Öt g├│c bß║▒ng \(60^{\circ}\)
b) Mß║Ęt b├¬n tß║Īo vß╗øi mß║Ęt ─æ├Īy mß╗Öt g├│c bß║▒ng \(45 ^{\circ}\).
-
Giß║Żi B├Āi 7.31 trang 63 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho khß╗æi l─āng trß╗ź ABC.A'B'C' c├│ ─æ├Īy l├Ā c├Īc tam gi├Īc ─æß╗üu cß║Īnh a, A'A = A'B = A'C = b. T├Łnh thß╗ā t├Łch cß╗¦a khß╗æi l─āng trß╗ź.
-
Giß║Żi B├Āi 7.32 trang 63 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
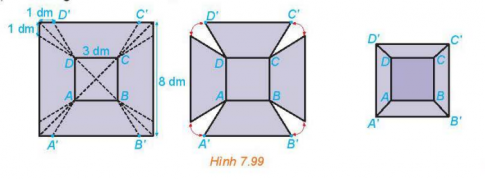
Tß╗½ mß╗Öt tß║źm t├┤n h├¼nh vu├┤ng c├│ cß║Īnh 8 dm, b├Īc H├╣ng cß║»t bß╗Å bß╗æn phß║¦n nhŲ░ nhau ß╗¤ bß╗æn g├│c, sau ─æ├│ b├Īc h├Ān c├Īc m├®p lß║Īi ─æß╗ā ─æŲ░ß╗Żc mß╗Öt chiß║┐c th├╣ng (kh├┤ng c├│ nß║»p ) nhŲ░ H├¼nh 7.99.
a) Giß║Żi th├Łch v├¼ sao chiß║┐c th├╣ng c├│ dß║Īng h├¼nh ch├│p cß╗źt.
b) T├Łnh cß║Īnh b├¬n cß╗¦a th├╣ng.
c) Hß╗Åi th├╣ng c├│ thß╗ā chß╗®a ─æŲ░ß╗Żc nhiß╗üu nhß║źt bao nhi├¬u l├Łt nŲ░ß╗øc?
-
Ba╠Ći t├ó╠Żp 7.33 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├¼nh ch├│p \(S.ABC\) c├│ \(SA \bot \left( {ABC} \right);\)\(AB = a;\)\(AC = a\sqrt 2 \) v├Ā \(\widehat {SBA} = 60^\circ \), \(\widehat {BAC} = 45^\circ \). T├Łnh theo \(a\) thß╗ā t├Łch khß╗æi ch├│p \(S.ABC\)?
-
Ba╠Ći t├ó╠Żp 7.34 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho khß╗æi ch├│p ─æß╗üu \(S.ABCD\) c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh vu├┤ng cß║Īnh bß║▒ng \(a\), g├│c giß╗»a mß║Ęt phß║│ng \(\left( {SCD} \right)\) v├Ā mß║Ęt phß║│ng \(\left( {ABCD} \right)\) bß║▒ng \(60^\circ \). T├Łnh theo \(a\) thß╗ā t├Łch khß╗æi ch├│p \(S.ABCD\)?
-
Ba╠Ći t├ó╠Żp 7.35 trang 38 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├¼nh l─āng trß╗ź \(ABC \cdot A'B'C'\) c├│ \(A'B'C'\) v├Ā \(AA'C'\) l├Ā hai tam gi├Īc ─æß╗üu cß║Īnh \(a\). Biß║┐t \(\left( {ACC'A'} \right) \bot \left( {A'B'C'} \right)\). T├Łnh theo \(a\) thß╗ā t├Łch khß╗æi l─āng trß╗ź \(ABC \cdot A'B'C'\)?
-
Ba╠Ći t├ó╠Żp 7.36 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho tß╗® diß╗ćn \(OABC\) c├│ \(OA = OB = OC = a\) v├Ā \(\widehat {AOB} = 90^\circ ;\) \(\widehat {BOC} = 60^\circ \); \(\widehat {COA} = 120^\circ \). T├Łnh theo \(a\) thß╗ā t├Łch khß╗æi tß╗® diß╗ćn \(OABC\)?
-
Ba╠Ći t├ó╠Żp 7.37 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├¼nh ch├│p c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh thoi t├óm \(O\), biß║┐t \(SO \bot \left( {ABCD} \right)\), \(AC = 2a\sqrt 3 ,BD = 2a\) v├Ā khoß║Żng c├Īch tß╗½ ─æiß╗ām \(A\) ─æß║┐n mß║Ęt phß║│ng \(\left( {SBC} \right)\) bß║▒ng \(\frac{{a\sqrt 3 }}{2}\). T├Łnh theo \(a\) thß╗ā t├Łch khß╗æi ch├│p \(S.ABCD\)?
-
Ba╠Ći t├ó╠Żp 7.38 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├¼nh ch├│p \(S.ABC\) c├│ \(SA \bot \left( {ABC} \right),SA = a\) v├Ā ─æ├Īy \(ABC\) l├Ā tam gi├Īc vu├┤ng tß║Īi \(A,AB = a,AC = a\sqrt 3 \). Kß║╗ \(AM\) vu├┤ng g├│c vß╗øi \(SB\) tß║Īi \(M,AN\) vu├┤ng g├│c vß╗øi \(SC\) tß║Īi \(N\). T├Łnh theo a thß╗ā t├Łch khß╗æi ch├│p \(S.AMN\)?
-
Ba╠Ći t├ó╠Żp 7.39 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├¼nh ch├│p \(S.ABC\) c├│ \(SA \bot \left( {ABC} \right)\) v├Ā \(\widehat {BAC} = {60^ \circ }\), biß║┐t diß╗ćn t├Łch c├Īc tam gi├Īc \(ABC,SAB\) v├Ā \(SAC\) lß║¦n lŲ░ß╗Żt l├Ā \(3\sqrt 3 ;9;12\). T├Łnh thß╗ā t├Łch khß╗æi ch├│p \(S.ABC\)?
-
Ba╠Ći t├ó╠Żp 7.40 trang 41 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
NgŲ░ß╗Øi ta cß║»t bß╗Å bß╗æn h├¼nh vu├┤ng c├╣ng k├Łch thŲ░ß╗øc ß╗¤ bß╗æn g├│c cß╗¦a mß╗Öt tß║źm t├┤n h├¼nh vu├┤ng c├│ cß║Īnh \(1{\rm{\;m}}\) ─æß╗ā g├▓ lß║Īi th├Ānh mß╗Öt chiß║┐c th├╣ng c├│ dß║Īng h├¼nh hß╗Öp chß╗» nhß║Łt kh├┤ng nß║»p. Hß╗Åi cß║Īnh cß╗¦a c├Īc h├¼nh vu├┤ng cß║¦n bß╗Å ─æi c├│ ─æß╗Ö d├Āi bß║▒ng bao nhi├¬u ─æß╗ā th├╣ng h├¼nh hß╗Öp nhß║Łn ─æŲ░ß╗Żc c├│ thß╗ā t├Łch lß╗øn nhß║źt?