Luyện tập 3 trang 103 SGK Toán 11 Tập 2 Cánh diều
Cho hình chóp \(S.ABC\) có \(SA = a\), góc giữa \(SA\) và \(mp\left( {ABC} \right)\) là \({60^ \circ }\). Gọi \(M,N\) lần lượt là trung điểm của cạnh \(SA\) và \(SB\). Chứng minh \(MN // \left( {ABC} \right)\) và tính \(d\left( {MN,\left( {ABC} \right)} \right)\)?
Hướng dẫn giải chi tiết Luyện tập 3
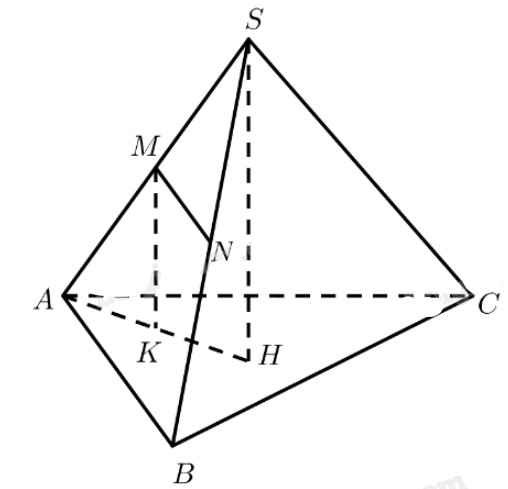
Ta có: \(M\) là trung điểm của \(SA\)
\(N\) là trung điểm của \(SB\)
\( \Rightarrow MN\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow MN // AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow MN // \left( {ABC} \right)\)
\( \Rightarrow d\left( {MN,\left( {ABC} \right)} \right) = d\left( {M,\left( {ABC} \right)} \right)\)
Gọi \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\)\( \Rightarrow SH \bot \left( {ABC} \right)\)
Qua \(M\) kẻ đường thẳng song song với \(SH\), cắt \(\left( {ABC} \right)\) tại \(K\)
\( \Rightarrow K \in AH,MK \bot \left( {ABC} \right) \Rightarrow d\left( {M,\left( {ABC} \right)} \right) = MK\)
\(\begin{array}{l}SH \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,HA} \right) = \widehat {SAH} = {60^ \circ }\\ \Rightarrow SH = SA.\sin \widehat {SAH} = \frac{{a\sqrt 3 }}{2}\end{array}\)
\(M\) là trung điểm của \(SA\), \(MK // SH\)
\( \Rightarrow MK\) là đường trung bình của \(\Delta SAH\)
\( \Rightarrow MK = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}\)
Vậy \(d\left( {MN,\left( {ABC} \right)} \right) = \frac{{a\sqrt 3 }}{4}\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 2 trang 102 SGK Toán 11 Tập 2 Cánh diều - CD
Hoạt động 3 trang 102 SGK Toán 11 Tập 2 Cánh diều - CD
Hoạt động 4 trang 103 SGK Toán 11 Tập 2 Cánh diều - CD
Luyện tập 4 trang 104 SGK Toán 11 Tập 2 Cánh diều - CD
Hoạt động 5 trang 105 SGK Toán 11 Tập 2 Cánh diều - CD
Luyện tập 5 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 1 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 2 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 3 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 4 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 5 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD
Bài tập 45 trang 109 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 46 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 47 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 48 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD





