Giải bài 3 trang 78 SGK Toán 10 Chân trời sáng tạo tập 1
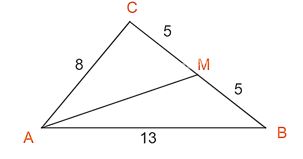
Cho tam giác ABC có \(a = 8,b = 10,c = 13.\) Tính các góc \(\widehat A,\widehat B,\widehat C.\)
a) Tam giác ABC có góc tù không?
b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.
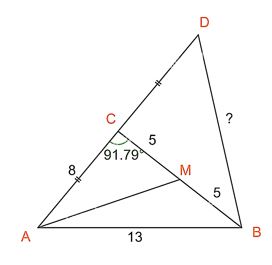
c) Lấy điểm D đối xứng với A qua C.
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
a)
Áp dụng hệ quả của định lí cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
Từ đó suy ra các góc \(\widehat A,\widehat B,\widehat C.\)
b) +) Tính AM: Áp dụng định lí cosin trong tam giác ACM:
\(A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\)
+) Tính diện tích:
Áp dụng công thức heron: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
+) Tính R: Áp dụng định lí sin: \(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}}\)
c) Áp dụng định lí cosin trong tam giác BCD:
\(B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\)
Lời giải chi tiết
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.13}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)
Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)
-- Mod Toán 10 HỌC247
-


Không sử dụng máy tính, thực hiện tính: \(\cos {12^0} - \cos {48^0} = \sin {18^0}\)
bởi thanh duy
 30/08/2022
Theo dõi (0) 1 Trả lời
30/08/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Giải bài 1 trang 78 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 78 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST