Giải bài 10 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1
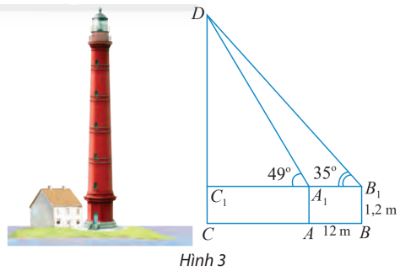
Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách \(AB = 12m\) cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là \(h = 1,2m.\) Gọi D là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao CD của tháp. Người ta do được \(\widehat {D{A_1}{C_1}} = {49^ \circ },\widehat {D{B_1}{C_1}} = {35^ \circ }.\) Tính chiều cao CD của tháp.
Hướng dẫn giải chi tiết Bài 10
Phương pháp giải
Bước 1: Tính góc \(\widehat {{A_1}D{B_1}}\) => Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) để tính \({A_1}D\)
Bước 2: Tính \({C_1}D\) từ đó suy ra chiều cao của tháp.
Lời giải chi tiết
Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)
-- Mod Toán 10 HỌC247
-


Không sử dụng máy tính, thực hiện tính: \(\displaystyle \cos {{22\pi } \over 3}\)
bởi Vương Anh Tú
 29/08/2022
Theo dõi (0) 1 Trả lời
29/08/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Giải bài 8 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 79 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST