Giải bài 7 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
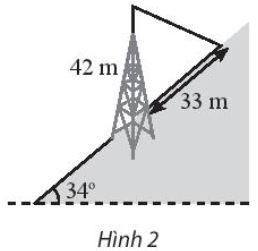
Một tháp viễn thông cao 42m được dựng thẳng đứng trên một sườn dốc \(34^\circ \)so với phương ngang. Từ đỉnh tháp người ta neo một sợi dây cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như hình 2. Tính chiều dài của sợi dây đó.
Hướng dẫn giải chi tiết Bài 7
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Lời giải chi tiết
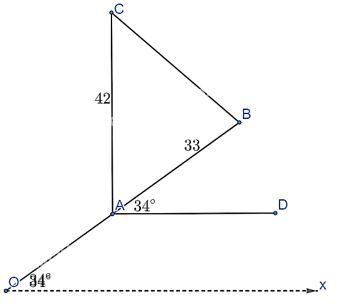
Ta có Ox song song với AD nên \(\widehat {AOx} = \widehat {BAD}\) (so le trong)
Mặt khác ta có : \(\widehat {CAB} + \widehat {BAD} = 90^\circ \Rightarrow \widehat {CAB} = 90^\circ - \widehat {BAD} = 56^\circ \)
Áp dụng đinhh lí côsin ta có :
\(BC = \sqrt {A{B^2} + A{C^2} - 2.AB.AC.\cos \widehat {BAC}} = \sqrt {{{33}^2} + {{42}^2} - 2.33.42.\cos 56^\circ } \simeq 36,1\)m
Vậy chiều dài sợi dây đó gần bằng 36,1 m
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.