Giải bài 4.39 tr 113 SBT Toán 10
Giải bất phương trình sau:
\(\frac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\)
Hướng dẫn giải chi tiết
\(\begin{array}{l}
\frac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1 \Leftrightarrow \frac{{{x^2} + x - 3}}{{{x^2} - 4}} - 1 \ge 0\\
\Leftrightarrow \frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} \ge 0\,\,\,\,\left( 1 \right)
\end{array}\)
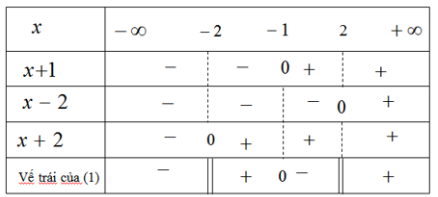
Bảng xét dấu vế trái của (1):
Vậy tập nghiệm của bất phương trình là : \(S = \left( { - 2; - 1} \right] \cup \left( {2; + \infty } \right)\)
-- Mod Toán 10 HỌC247
-


Giải bất phương trình -2x + 3 > 0.
bởi Ho Ngoc Ha
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Tập nghiệm của hệ bất phương trình
bởi Phạm Đức
 17/02/2021
Câu 171
17/02/2021
Câu 171 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bất phương trình (x-2)(x-m)>0
bởi Huu Ha Nguyen
 05/02/2021
05/02/2021
Giải bất phương trình (x-2)(x-m)>0
Theo dõi (0) 0 Trả lời -


Giải bất phương trình:
bởi Yến Nhi
 27/01/2021
27/01/2021
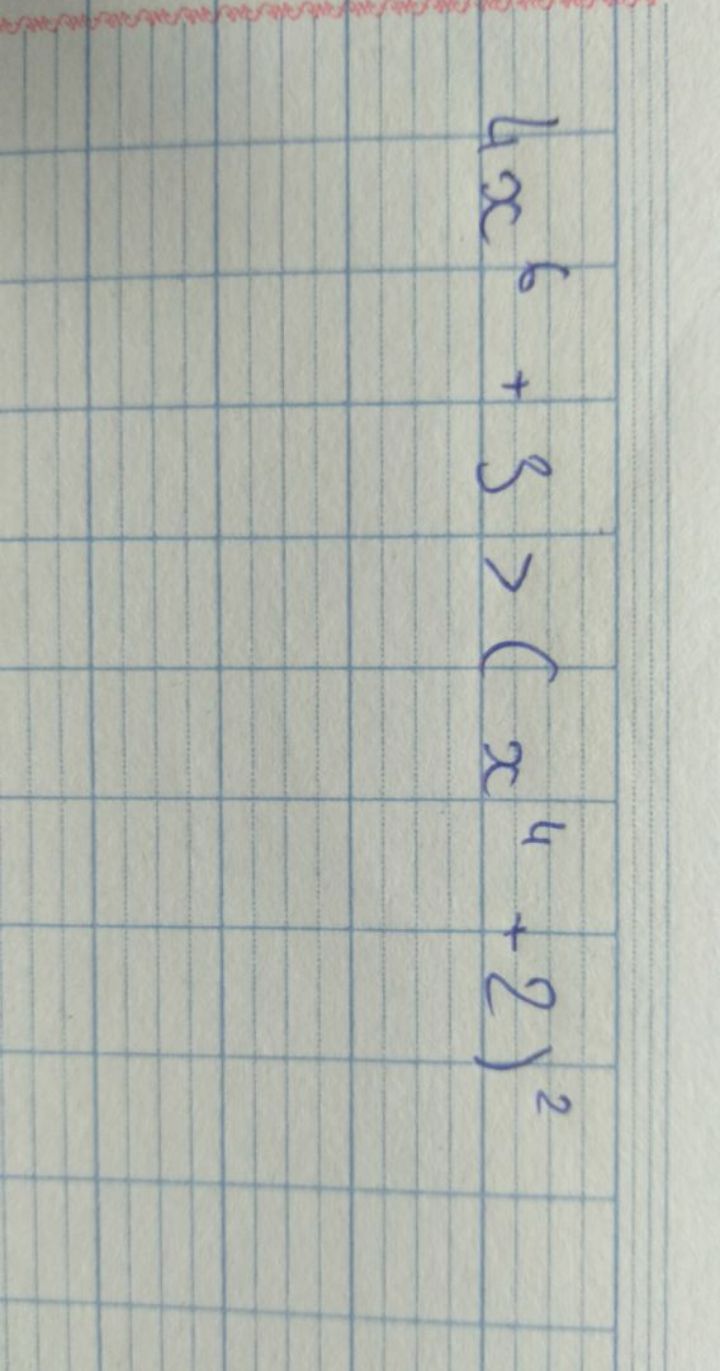 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4.37 trang 112 SBT Toán 10
Bài tập 4.38 trang 112 SBT Toán 10
Bài tập 4.40 trang 113 SBT Toán 10
Bài tập 4.41 trang 113 SBT Toán 10
Bài tập 4.42 trang 113 SBT Toán 10
Bài tập 4.43 trang 113 SBT Toán 10
Bài tập 4.44 trang 113 SBT Toán 10
Bài tập 4.45 trang 113 SBT Toán 10
Bài tập 32 trang 126 SGK Toán 10 NC
Bài tập 33 trang 126 SGK Toán 10 NC
Bài tập 34 trang 126 SGK Toán 10 NC
Bài tập 35 trang 126 SGK Toán 10 NC
Bài tập 36 trang 127 SGK Toán 10 NC
Bài tập 37 trang 127 SGK Toán 10 NC
Bài tập 38 trang 127 SGK Toán 10 NC
Bài tập 39 trang 127 SGK Toán 10 NC