Bài tập 35 trang 126 SGK Toán 10 NC
Giải các hệ phương trình
a) \(\left\{ \begin{array}{l}
\left( {x - 3} \right)\left( {\sqrt 2 - x} \right) > 0\\
\frac{{4x - 3}}{2} < x + 3
\end{array} \right.\)
b) \(\left\{ \begin{array}{l}
\frac{2}{{2x - 1}} \le \frac{1}{{3 - x}}\\
\left| x \right| < 1
\end{array} \right.\)
Hướng dẫn giải chi tiết
a)
\(\left\{ {\begin{array}{*{20}{l}}
{\left( {x - 3} \right)\left( {\sqrt 2 - x} \right) > 0\,\,\,\left( 1 \right)}\\
{\frac{{4x - 3}}{2} < x + 3\,\,\,\left( 2 \right)}
\end{array}} \right.\)
Giải (1):
Bảng xét dấu
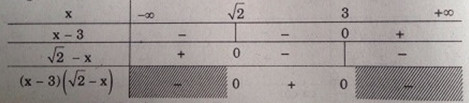
Suy ra tập nghiệm \({S_1} = \left( {\sqrt 2 ;3} \right)\)
Giải (2):
\(\left( 2 \right) \Leftrightarrow 4x - 3 < 2x + 6 \Leftrightarrow 2x < 9 \Leftrightarrow x < \frac{9}{2}\)
Vậy \(S = {S_1} \cap {S_2} = \left( {\sqrt 2 ;3} \right)\)
b)
\(\left\{ {\begin{array}{*{20}{l}}
{\frac{2}{{2x - 1}} \le \frac{1}{{3 - x}}\,\,\,\left( 1 \right)}\\
{ - 1 < x < 1}
\end{array}} \right.\)
Giải (1):
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{2}{{2x - 1}} \le \frac{1}{{3 - x}}\\
\Leftrightarrow \frac{2}{{2x - 1}} - \frac{1}{{3 - x}} \le 0
\end{array}\\
\begin{array}{l}
\Leftrightarrow \frac{{6 - 2x - 2x + 1}}{{\left( {2x - 1} \right)\left( {3 - x} \right)}} \le 0\\
\Leftrightarrow \frac{{ - 4x + 7}}{{\left( {2x + 1} \right)\left( {3 - x} \right)}} \le 0
\end{array}
\end{array}\)
Bảng xét dấu
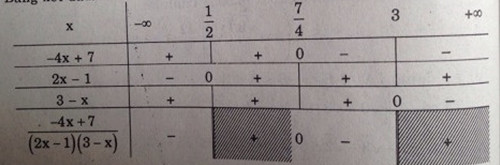
Suy ra tập nghiệm \({S_1} = \left( { - \infty ;\frac{1}{2}} \right) \cup \left[ {\frac{7}{4};3} \right)\)
Kết hợp với - 1 < x < 1 ta có tập nghiệm của hệ là \(S = \left( { - 1;\frac{1}{2}} \right)\)
-- Mod Toán 10 HỌC247
-


tim m để bpt m2x+3<mx+4 có nghiệm
Tìm m để (m+1)x2+ mx+m<0 với mọi x thuộc R
Theo dõi (0) 0 Trả lời -


Tìm m để bất phương trình m^2x+3 < mx+4 có nghiệm
bởi Lâm tâm như Như
 13/02/2019
13/02/2019
tim m để bpt m2x+3<mx+4 có nghiệm
Tìm m để (m+1)x2+ mx+m<0 với mọi x thuộc R
Theo dõi (0) 0 Trả lời -


Giải và biện luận bất phương trình sau:
(m+1)x+m< 3m+4
Theo dõi (0) 2 Trả lời -


Bài 32 trang 114 sách bài tập Toán 10
bởi Hy Vũ
 01/10/2018
Bài 32 (SBT trang 114)
01/10/2018
Bài 32 (SBT trang 114)Giải các bất phương trình sau :
\(\dfrac{x^2+x-3}{x^2-4}\ge1\)
Theo dõi (0) 1 Trả lời





