Bài tập 1 trang 7 SGK Hình học 10

Câu a:

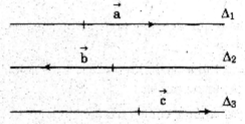
Ta gọi \({\Delta _1},{\Delta _2},{\Delta _3}\) lần lượt là giá của \(\overrightarrow a ,\overrightarrow b \) và \(\overrightarrow c \). Vì \(\overrightarrow a ,\overrightarrow b \)cùng phương với \(\overrightarrow c \) nên \({\Delta _1}\) song song hoặc trùng \({\Delta _3}\) và \({\Delta _2}\) song song hoặc trùng \({\Delta _3}\), từ đấy suy ra \({\Delta _1}\)song song hoặc trùng \({\Delta _2}\), tức là \(\overrightarrow a \) và \(\overrightarrow b \)  cùng phương.

Vậy khẳng định đã cho là đúng.

Câu b:

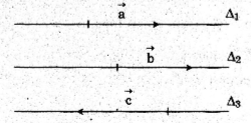
 Nếu \(\overrightarrow a \) ngược hướng với \(\overrightarrow b \) thì \(\overrightarrow b \) và \(\overrightarrow c \) cùng hướng, ta có mâu thuẫn

Vậy \(\overrightarrow a \) và \(\overrightarrow b \)cùng hướng.

-- Mod Toán 10 HỌC247