Giải bài 1.7 tr 10 SBT Hình học 10
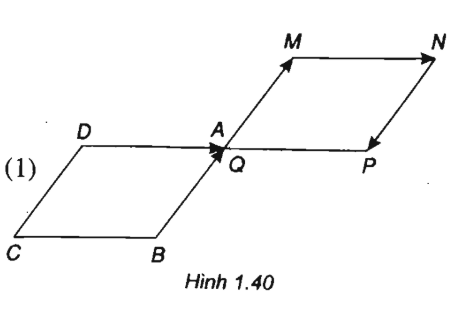
Cho hình bình hành ABCD. Dựng \(\overrightarrow {AM} = \overrightarrow {BA} ,\overrightarrow {MN} = \overrightarrow {DA} ,\overrightarrow {NP} = \overrightarrow {DC} ,\overrightarrow {PQ} = \overrightarrow {BC} \). Chứng minh \(\overrightarrow {AQ} = \overrightarrow 0 \) .
Hướng dẫn giải chi tiết
+ Trên tia BA lấy điểm M sao cho BA = AM, khi đó \(\overrightarrow {AM} = \overrightarrow {BA} \).
+ Qua M kẻ đường thẳng song song DA, lấy điểm N sao cho MN = DA và \(\overrightarrow {MN}\) cùng hướng \(\overrightarrow {DA}\). Khi đó ta được \(\overrightarrow {MN} = \overrightarrow {DA} \).
+ Qua N kẻ đường thẳng song song DC, lấy điểm P sao cho NP = DC và \(\overrightarrow {NP}\) cùng hướng \(\overrightarrow {DC}\). Khi đó ta được \(\overrightarrow {NP} = \overrightarrow {DC} \).
+ Qua P kẻ đường thẳng song song BC, lấy điểm Q sao cho PQ = BC và \(\overrightarrow {PQ}\) cùng hướng \(\overrightarrow {BC}\). Khi đó ta được \(\overrightarrow {PQ} = \overrightarrow {BC} \).
Lại có \(\overrightarrow {MA} = \overrightarrow {DB} \) và \(\overrightarrow {NP} = \overrightarrow {DC} = \overrightarrow {AB} \).
Suy ra AM = NP và AM//NP. Vậy tứ giác AMNP là hình bình hành.
Ta có \(\overrightarrow {PQ} = \overrightarrow {BC} \); \(\overrightarrow {MN} = \overrightarrow {DA} = \overrightarrow {CB} \)
Suy ra PQ = MN và PQ//MN.
Vậy tứ giác MNPQ là hình bình hành (2).
Từ (1) và (2) suy ra A≡Q hay \(\overrightarrow {AQ} = \overrightarrow 0 \).
-- Mod Toán 10 HỌC247
-


Tìm vecto bằng với vecto EF trong lục giác đều ABCDEF
bởi My Hien
 02/10/2018
02/10/2018
1)cho lục giác đều ABCDEF có tâm o.tìm các véc tơ bằng véc tơ EF?
2)cho hình vuông ABDC cạnh bằng a có điểm o. véc tơ AB+AC+AD=2AC và tính |BC+_BA|?
3)cho véc tơ a=(1;2) véc tơ b= (4;3) véc tơ c=(-5)
Theo dõi (0) 1 Trả lời -


Tìm các bộ ba vecto đôi một bằng nhau trong tam giác ABC với trung tuyến AD, BE, CF?
bởi Mai Anh
 02/10/2018
02/10/2018
Hãy vẽ một tam giác ABC với trung tuyến AD, BE, CF, rồi chỉ ra các bộ ba vectơ khác và đôi một bằng nhau (các vectơ này có điểm đầu và điểm cuối được lấy trong sáu điểm A, B, C, D, E, F). Nếu G là trọng tâm tam giác ABC thì có thể viết hay không? Vì sao?
Theo dõi (0) 1 Trả lời -


Nêu các định nghĩa về vecto
bởi trang lan
 07/11/2018
07/11/2018
Nêu các định lý về vectơ
Theo dõi (0) 1 Trả lời