Giải bài 4 tr 7 sách GK Toán Hình lớp 10
Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vec to khác \(\vec 0\) và cùng phương với \(\overrightarrow {OA}\)
b) Tìm các véc tơ bằng véc tơ \(\overrightarrow {AB}\)
Hướng dẫn giải chi tiết bài 4
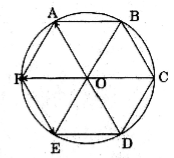
Tâm O của lục giác đều chính là tâm đường tròn đi qua sáu điểm A, B, C, D, E, F. Vì ABCDEF là lục giác đều nên các tứ giác ABCO, BCDO, CDEO, DEFO, EFAO, FABO là các hình thoi bằng nhau.
Câu a:
Ta thấy giá của các vecto: \(\overrightarrow {CD} ,\overrightarrow {DO} ,\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {DA} ,\overrightarrow {{\rm{EF}}} ,\overrightarrow {FE} ,\overrightarrow {{\rm{BC}}} ,\overrightarrow {{\rm{CB}}} \) song song hoặc trùng với giá của vecto \(\overrightarrow {OA} \), do vậy chín vecto trên cùng phương với vecto \(\overrightarrow {OA} \).
Câu b:
Do các tứ giác nói trên là những hình thoi bằng nhau nên:
\[\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {FO} } \right| = \left| {\overrightarrow {OC} } \right| = \left| {\overrightarrow {ED} } \right|\,\,\,\,\,\,(1)\]
Mặt khác dễ thấy rằng các vecto \(\overrightarrow {AB} ,\overrightarrow {FO} ,\overrightarrow {\,\,OC} ,\,\,\,\overrightarrow {ED} \) là cùng hướng (2)
Từ (1) và (2) ta có những vecto bằng vecto \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {\,\,OC} ,\,\,\,\overrightarrow {ED} .\)
-- Mod Toán 10 HỌC247
Để luyện tập thêm dạng bài tương tự như Bài tập 4 trang 7 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.
-
Câu 1:
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?
- A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các đỉnh của ngũ giác.
- B. Có 5 vectơ gốc O có độ dài bằng nhau.
- C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác.
- D. Các vectơ khác 0→ có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau
.PNG)
-
Tìm các bộ ba vecto đôi một bằng nhau trong tam giác ABC với trung tuyến AD, BE, CF?
bởi Mai Anh
02/10/2018
Hãy vẽ một tam giác ABC với trung tuyến AD, BE, CF, rồi chỉ ra các bộ ba vectơ khác và đôi một bằng nhau (các vectơ này có điểm đầu và điểm cuối được lấy trong sáu điểm A, B, C, D, E, F). Nếu G là trọng tâm tam giác ABC thì có thể viết hay không? Vì sao?
Theo dõi (0) 1 Trả lời -
Nêu các định nghĩa về vecto
bởi trang lan
07/11/2018
Nêu các định lý về vectơ
Theo dõi (0) 1 Trả lời -
Giúp em giải bài này được không mọi người
bởi Nguyễn Hậu
27/07/2018
57 phút trước (06:50)
Cho tam giác ABC có trực tâm H và nội tiếp đường tròn tâm O. Gọi B', A' lần lượt là điểm đối xứng với B và A qua O. M là trung điểm của BC
a) Cmr: Vectơ B'C = Vectơ AH
b) Cmr: Vectơ HM = Vectơ MA
c) AH cắt BC tại I và cắt (O) tại K. Cmr: Vectơ IH = Vectơ KI
Câu hỏi tương tự Đọc thêm Báo cáo
Theo dõi (0) 0 Trả lời
Được đề xuất cho bạn
