Giải bài 1.5 tr 10 SBT Hình học 10
Cho tứ giác ABCDABCD, chứng minh rằng \(\overrightarrow {AB} = \overrightarrow {DC} \) thì \(\overrightarrow {AD} = \overrightarrow {BC} \).
Hướng dẫn giải chi tiết
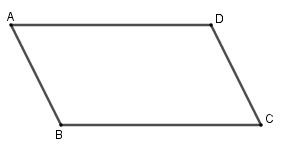
Tứ giác ABCD có \(\overrightarrow {AB} = \overrightarrow {DC} \) nên AB = DC và AB//DC. Do đó ABCDlà hình bình hành, suy ra \(\overrightarrow {AD} = \overrightarrow {BC} \).
-- Mod Toán 10 HỌC247
-
Bài 1.5 trang 12 sách bài tập Toán 10
bởi Nguyễn Anh Hưng
02/10/2018
Bài 1.5 (STB trang 12)Cho tứ giác ABCD, chứng minh rằng nếu : \(\overrightarrow{AB}=\overrightarrow{DC}\) thì \(\overrightarrow{AD}=\overrightarrow{BC}\) ?
Theo dõi (0) 1 Trả lời -
Bài 1.4 trang 12 sách bài tập Toán 10
bởi hi hi
02/10/2018
Bài 1.4 (STB trang 12)Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm các cạnh AB và AC. So sánh độ dài của hai vectơ \(\overrightarrow{NM}\) và \(\overrightarrow{BC}\). Vì sao có thể nói hai vectơ này cùng phương ?
Theo dõi (0) 1 Trả lời -
Bài 1.3 trang 12 sách bài tập Toán 10
bởi Anh Trần
02/10/2018
Bài 1.3 (STB trang 12)Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh \(\overrightarrow{NP}=\overrightarrow{MQ}\) và \(\overrightarrow{PQ}=\overrightarrow{NM}\) ?
Theo dõi (0) 1 Trả lời
