-
Đáp án C
Phương pháp: Sgk 12 trang 25
Cách giải: Tận dụng thời cơ Nhật đầu hàng đồng minh không điều kiện, vào giữa tháng 8-1945, nhân dân Đông Nam Á đứng lên đấu tranh, có ba nước đã giành nổi dậy và tuyên bố độc lập là :In-đô-nê-xi-a (17-8-1945), Việt Nam (2-9-1945), Lào (12-10-1945)
Câu hỏi:Cho tam giác ABC vuông tại A có AC=3a, AB=4a. Cho tam giác này quay quanh đường thẳng BC, tính thể tích V của khối tròn xoay thu được.
- A. \(V = \frac{{84\pi {a^2}}}{{15}}\)
- B. \(V = \frac{{120\pi {a^2}}}{{27}}\)
- C. \(V = \frac{{144\pi {a^2}}}{{15}}\)
- D. \(V = \frac{{84\pi {a^2}}}{{25}}\)
Đáp án đúng: C
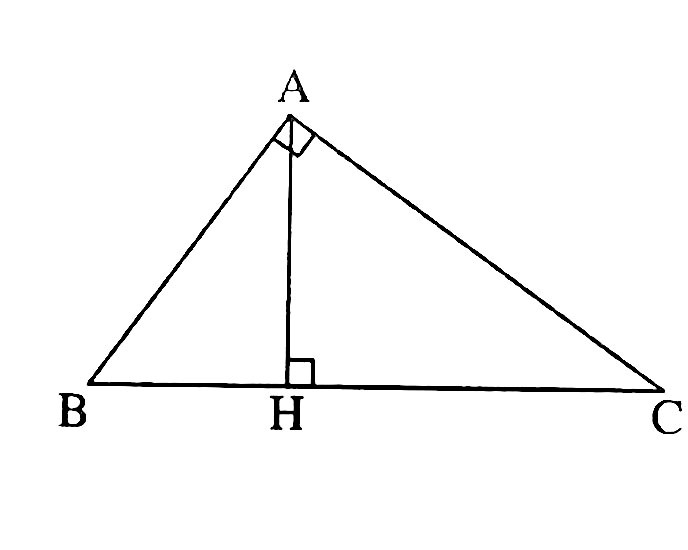
Kẻ đường cao AH của ∆ABC khi quay quanh đường thẳng BC miền tam giác ABC sinh ra hai khối nón chung đáy, bán kính đáy là R = AH và chiều cao lần lượt là HB và HC.
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{16{a^2}}} + \frac{1}{{9{a^2}}} = \frac{{25}}{{144{a^2}}}.\)
Suy ra \(A{H^2} = \frac{{25}}{{144{a^2}}}.\)
Thể tích khối tròn xoay sinh ra là:
\(V = {V_1} + {V_2} = \frac{1}{3}\pi A{H^2}.\left( {HB + HC} \right) = \frac{1}{3}\pi .\frac{{144{a^2}}}{{25}}.5a = \frac{{144\pi {a^2}}}{{15}}.\)
\(\left( {HB + HC = BC = 5a} \right).\)
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ MẶT NÓN, HÌNH NÓN, KHỐI NÓN
- Trong không gian, cho tam giác ABC là tam giác vuông cân tại A, gọi I là trung điểm của BC, BC=2. Tính diện tích xung quanh của hình nón nhận được khi quay tam giác ABC quanh trục AI
- Cho tam giác ABC vuông tại A, AB=3a, AC=4a. Gọi M là trung điểm của AC. Khi qua quanh AB, các đường gấp khúc AMB, ACB sinh ra các hình nón
- Cho hình chóp đều S.ABC. Gọi G là trọng tâm tam giác ABC. Quay các cạnh của hình chóp đã cho quanh trục SG. Hỏi có tất cả bao nhiêu hình nón tạo thành?
- Cho hình tròn bán kính R=2. Người ta cắt bỏ đi frac{1}{4} hình tròn rồi dùng phần còn lại để dán lại tạo nên một mặt xung quanh của hình nón (H)
- Tính diện tích xung quanh của hình nón tròn xoay tạo thành khi quay tam giác ABC quanh cạnh AC biết tam giác ABC vuông tại A có AB=6, AC=8
- Trong các hình nón nội tiếp một hình cầu có bán kính bằng 3, tính bán kính mặt đáy của hình nón có thể tích lớn nhất
- Tính diện tích xung quanh S của hình nón có độ dài đường sinh bằng 2 cm, góc ở đỉnh bằng 60 độ
- Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Tìm số đo góc ở đỉnh của hình nón
- Tính thể tích khối nón có độ dài đường sinh l=2a và góc ở đinh 60 độ
- Cho khối nón đỉnh O, trục OI. Mặt phẳng trung trực OI chia khối nón thành hai phần. Tính tỉ số thể tích của hai phần






