-
Câu hỏi:
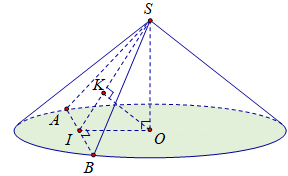
Cho hình nón tròn xoay có chiều cao \(h = 20\,\left( {{\rm{cm}}} \right)\), bán kính đáy \(r = 25\,\left( {{\rm{cm}}} \right)\). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là \(12\,\left( {{\rm{cm}}} \right)\). Tính diện tích của thiết diện đó.
- A. \(S = 500\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
- B. \(S = 400\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
- C. \(S = 300\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
- D. \(S = 406\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Lời giải tham khảo:
Đáp án đúng: A
Theo bài ra ta có \(AO = r = 25;SO = h = 20;\,OK = 12\) (Hình vẽ).
Lại có \(\frac{1}{{O{K^2}}} = \frac{1}{{O{I^2}}} + \frac{1}{{O{S^2}}} \Rightarrow OI = 15\,\left( {{\rm{cm}}} \right)\)
\(AB = 2AI = \sqrt {{{25}^2} - {{15}^2}} = 40\,\left( {{\rm{cm}}} \right);\;SI = \sqrt {S{O^2} + O{I^2}} = 25\,\left( {{\rm{cm}}} \right) \Rightarrow {S_{\Delta SAB}} = \frac{1}{2}.25.40 = 500\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho hình lập phương có cạnh bằng 40 cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diệ
- Cho tam giác SAB vuông tại A, \(\widehat {ABS} = 60^0 \), đường phân giác trong của \(\widehat {ABS}\) cắt SA tại đi�
- Cho lăng trụ tam giác đều có cạnh đáy bằng \(a\) cạnh bên bằng \(b\).
- Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh bằng \(2\sqrt 3 \,\left( {{\rm{cm}}} \right)\) với AB là đ�
- Cho hình nón tròn xoay có chiều cao \(h = 20\,\left( {{\rm{cm}}} \right)\), bán kính đáy \(r = 25\,\left( {{\rm{cm}}} \right)\).
- Cho hình trụ có hai đáy là hai hình tròn (O) và (O]), chiều cao \(R\sqrt 3 \) và bán kính đáy R.
- Cho hình thang ABCD vuông tại A và B với \(AB = BC = \frac{{AD}}{2} = a\) .
- Cho hình tứ diện ABCD có M, N lần lượt là trung điểm của AB, BD.
- Hình nón có thiết diện qua trục là tam giác đều và có thể tích \(V = \frac{{\sqrt 3 }}{3}\pi {a^3}\).
- Cho một khối nón có chiều cao bằng 4cm, độ dài đường sinh 5cm. Tính thể tích khối nón này.
- Cho hình lập phương ABCD.ABCD cạnh bằng \(3a\).
- Một hình nón có đường sinh bằng \(a\) và góc ở đỉnh bằng \(90^0\).
- Cho một khối trụ có độ dài đường sinh bằng 10 cm. Biết thể tích khối trụ bằng \(90\pi {\rm{ c}}{{\rm{m}}^3}\).
- Tính diện tích xung quanh của hình nón S có đỉnh là tâm hình vuông A'B'C'D' và đường tròn đáy ngoại tiếp hình vuông ABCD
- Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy, \(SA=a, AD = 5a,\;AB = 2a.
- Cho mặt cầu \((S_1)\) có bán kính \(R_1\), mặt cầu \((S_2)\) có bán kính \(R_2=2R_1\).
- Cho tứ diện đều S.ABC cạnh \(a\).
- Cho hình chóp S.ABC có tam giác ABC vuông tại B, SA vuông góc với mặt phẳng (ABC). \(SA=5, AB=3, BC=4\).
- Một hình trụ có bán kính đáy là 2 cm.
- Cắt một khối trụ cho trước thành hai phần thì được hai khối trụ mới có tổng diện tích toàn phần nhiều hơn diện
- Cho hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB.
- Thể tích của khối nón có độ dài đường sinh bằng \(2a\) và diện tích xung quanh bằng \(2\pi {a^2}\) là
- Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng \(3a\).
- Cho tam giác ABC vuông tại A, \(AB=6cm, AC=8cm\).
- Cho mặt cầu \(S(O;R)\) và điểm A cố định nằm ngoài mặt cầu với \(OA=d\).
- Tính diện tích toàn phần S_tp của hình trụ khi quay hình chữ nhật quanh trục MN
- Cho hình nón có đường sinh bằng đường kính đáy và bằng 2. Bán kính của mặt cầu ngoại tiếp hình nón đó là:
- Cho tam giác ABC có \(\widehat {ABC} = 45^\circ \widehat {,ACB} = 30^\circ ,AB = \frac{{\sqrt 2 }}{2}\).
- Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, B.
- Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật có và thuộc hai đáy của hình trụ,
- Cho mặt cầu bán kính R ngoại tiếp một hình hộp chữ nhật có các kích thước \(a, 2a, 3a\).
- Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2.
- Cho hình chóp S.ABCD có đáy là hình vuông, \(BD=2a\).
- Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính, \(R=3cm\), góc ở đỉnh hình nón là \(\varphi = 120^0 \).
- Cho hình lăng trụ đứng ABC.ABC có đáy là tam giác vuông cân tại A, \(AB = AC = a,AA = \sqrt 2 a\).
- Cho hình chóp tam giác đều S.ABC.
- Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng \(a\). Cạnh bên SA vuông góc với mặt đáy và \(SA = a\sqrt 2 \).
- Cho hình lăng trụ lục giác đều có cạnh đáy bằng \(a\sqrt 2 \), cạnh bên bằng \(2a\sqrt 2 \).
- Một cái nồi nấu nước người ta làm dạng hình trụ, chiều cao của nồi là 60cm, diện tích đáy \(900\pi cm^2\).
- Cho hình lăng trụ tam giác đều ABCD.ABCD có 9 cạnh bằng nhau và bằng \(2a\).