Phương pháp giải bài tập về năng lượng trong mạch dao động LC môn Vật Lý 12 năm 2021-2022

1.1. Năng lượng điện từ

Tổng năng lượng điện trường tụ điện và năng lượng từ trường trên cuộn cảm gọi là năng lượng điện từ.

a. Năng lượng điện từ: \(\text{W}={{\text{W}}_{C}}+{{\text{W}}_{L}}=\frac{1}{2}C.U_{0}^{2}=\frac{1}{2}L.I_{0}^{2}=\frac{1}{2}\frac{q_{0}^{2}}{C}\)

b. Năng lượng điện trường: \({{\text{W}}_{C}}=\frac{1}{2}C.{{u}^{2}}=\frac{1}{2}\frac{{{q}^{2}}}{C}=\frac{1}{2C}q_{0}^{2}{{\cos }^{2}}\left( \omega t+\varphi  \right)\)

c. Năng lượng từ trường: \({{\text{W}}_{L}}=\frac{1}{2}L{{i}^{2}}=\frac{1}{2C}q_{0}^{2}{{\sin }^{2}}\left( \omega t+\varphi  \right)\)

Nhận xét:

+ Trong quá trình dao động điện từ, có sự chuyển đổi từ năng lượng điện trường thành năng lượng từ trường và ngược lại, nhưng tổng của chúng thì không đổi.

+ Mạch dao động có tần số góc \(\omega \), tần số f và chu kỳ T thì \({{W}_{L}}\) và \({{W}_{C}}\) biến thiên với tần số góc \(2\omega \), tần số 2f và chu kỳ T/2.

+ Trong một chu kỳ có 4 lần \({{W}_{L}}={{W}_{C}}\), khoảng thời gian giữa hai lần liên tiếp để \({{W}_{L}}={{W}_{C}}\) là T/4.

+ Thời gian từ lúc \({{W}_{L}}={{W}_{L\max }}\left( {{W}_{C}}={{W}_{C\max }} \right)\) đến lúc \({{W}_{L}}={{W}_{L\max }}/2\left( {{W}_{C}}={{W}_{C\max }}/2 \right)\) là T/8.

+ Khi \({{W}_{L}}=n.{{W}_{C}}\Rightarrow q=\pm \frac{{{Q}_{0}}}{\sqrt{n+1}};u=\pm \frac{{{U}_{0}}}{\sqrt{n+1}};i=\pm \frac{{{I}_{0}}}{\sqrt{\frac{1}{n}+1}}\)

* Cách cấp năng lượng ban đầu cho mạch dao động:

- Cấp năng lượng ban đầu cho tụ: \(W=\frac{1}{2}C{{E}^{2}}=\frac{1}{2}C{{U}_{0}}\); Với E: là suất điện động của nguồn

- Cấp năng lượng ban đầu cho cuộn dây: \(W=\frac{1}{2}L{{I}_{0}}=\frac{1}{2}L{{\left( \frac{E}{r} \right)}^{2}}\); Với r là điện trở trong của nguồn

1.2. Các hệ thức độc lập:

a) \(Q_{0}^{2}={{q}^{2}}+{{\left( \frac{i}{\omega } \right)}^{2}}\Rightarrow {{\left( \frac{q}{{{Q}_{0}}} \right)}^{2}}+{{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}=1\)  hay \({{\left( \frac{u}{{{U}_{0}}} \right)}^{2}}+{{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}=1\)

b)

\(W={{W}_{C}}+{{W}_{L}}\Rightarrow \left\{ \begin{align} & {{u}^{2}}+\frac{L}{C}{{i}^{2}}=U_{0}^{2}\Rightarrow i=\sqrt{\frac{C}{L}\left( U_{0}^{2}-{{u}^{2}} \right)} \\ & {{i}^{2}}+\frac{C}{L}{{u}^{2}}=I_{0}^{2}\Rightarrow u=\sqrt{\frac{L}{C}\left( I_{0}^{2}-{{i}^{2}} \right)} \\ \end{align} \right.\)

1.3. Công suất bù đắp do hao phí khi mạch dao động có điện trở thuần \(\mathbf{R}=\mathbf{0}\):

Dao động sẽ tắt dần. Để duy trì dao động cần cung cấp cho mạch một năng lượng có công suất:

\(P={{I}^{2}}.R=\frac{{{\omega }^{2}}.{{C}^{2}}.U_{0}^{2}}{2}.R=\frac{U_{0}^{2}.R.C}{2.L}\Rightarrow W=P.t\)

Ví dụ 1: Một mạch dao động gồm 1 tụ điện \(C=20nF\)  và 1 cuộn cảm \(L=8\mu H\) điện trở không đáng kể. Điện áp cực đại ở hai đầu tụ điện là \({{U}_{0}}=1,5V\). Cường độ dòng hiệu dụng chạy trong mạch.

A. 48mA                         

B. 65mA                      

C. 53mA                      

D. 72mA

Hướng dẫn giải

Theo định luật bảo toàn năng lượng ta có: \(\frac{1}{2}C.U_{0}^{2}=\frac{1}{2}L.I_{0}^{2}\)

\(\Rightarrow {{I}_{0}}={{U}_{0}}\sqrt{\frac{C}{L}}\Rightarrow I=\frac{{{U}_{0}}}{\sqrt{2}}\sqrt{\frac{C}{L}}=0,053A=53mA\)

→ Chọn đáp án C

Ví dụ 2: Biết khoảng thời gian giữa 2 lần liên tiếp năng lượng điện trường bằng năng lượng từ trường của mạch dao động điện từ tự do LC là \({{10}^{7}}\text{ }s\). Tần số dao động riêng của mạch là:

A. 2 MHz                        

B. 25 MHz                   

C. 2,5 MHz                  

D. 210 MHz

Hướng dẫn giải

Ta có \(t=\frac{T}{4}\Rightarrow T=4t={{4.10}^{-7}}s\Rightarrow f=\frac{1}{T}=2,5MHz\)

→ Chọn đáp án C

Ví dụ 3: Một mạch dao động gồm một tụ có điện dung \(C=10\mu F\) và một cuộn cảm có độ tự cảm \(L=1H\), lấy \({{\pi }^{2}}=10\). Khoảng thời gian ngắn nhất tính từ lúc năng lượng điện trường đạt cực đại đến lúc năng lượng từ bằng một nửa năng lượng điện trường cực đại là

A. \(\frac{1}{400}s\)      

B. \(\frac{1}{300}s\)   

C. \(\frac{1}{200}s\)   

D. \(\frac{1}{100}s\)

Hướng dẫn giải

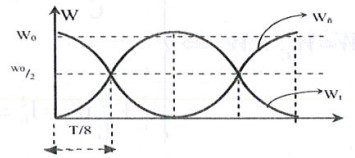
Lúc năng lượng điện trường cực đại nghĩa là \({{\text{W}}_{d}}={{\text{W}}_{d\max }}=W\)

Lúc năng lượng điện trường bằng một nửa điện trường cực đại tức là \({{\text{W}}_{d}}=\frac{{{\text{W}}_{d\max }}}{2}=\frac{W}{2}\)

Quan sát đồ thị bên

→ Chọn đáp án A

Ví dụ 4: Cường độ dòng điện trong mạch dao động LC có biểu thức \(i=9cos\omega t\text{ }\left( mA \right)\). Vào thời điểm năng lượng điện trường bằng 8 lần năng lượng từ trường thì cường độ dòng điện i bằng

A. \(\pm 3mA\)               

B. \(\pm 1,5\sqrt{2}mA\)                                  

C. \(\pm 2\sqrt{2}mA\)           

D. \(\pm 1mA\)

Hướng dẫn giải

\(\left\{ \begin{align} & {{W}_{d}}=8.{{W}_{t}} \\ & W={{W}_{d}}+{{W}_{t}} \\ \end{align} \right.\Rightarrow W=9{{W}_{t}}\Rightarrow \frac{1}{2}L.I_{0}^{2}=9.\frac{1}{2}L{{i}^{2}}\Rightarrow I_{0}^{2}=9{{i}^{2}}\Rightarrow i=\pm \frac{{{I}_{0}}}{3}=\pm 3mA\)

→ Chọn đáp án A

Ví dụ 5: Tụ điện của mạch dao động có điện dung \(C=1\mu F\), ban đầu được điện tích đến hiệu điện thế 100V, sau đó cho mạch thực hiện dao động điện từ tắt dần. Năng lượng mất mát của mạch từ khi bắt đầu thực hiện dao động đến khi dao động điện từ tắt hẳn là bao nhiêu?

A. \(\Delta W=10mJ\)     

B. \(\Delta W=10kJ\)   

C. \(\Delta W=5mJ\)  

D. \(\Delta W=5kJ\)

Hướng dẫn giải

Năng lượng đến lúc tắt hẳn: \(\Delta P=P=\frac{1}{2}C.U_{0}^{2}=\frac{1}{2}{{10}^{-6}}{{.100}^{2}}={{5.10}^{-3}}J=5mJ\)

→ Chọn đáp án C

Ví dụ 6: Một mạch dao động điện từ tự do \(L=0,1H\) và \(C=10\mu F\). Tại thời điểm cường độ dòng điện qua cuộn cảm là 0,03A thì điện áp ở hai bản tụ là 4V. Cường độ dòng điện cực đại trong mạch là

A. 0,05 A                        

B. 0,03 A                     

C. 0,003 A                   

D. 0,005 A

Hướng dẫn giải

Ta có: \(\frac{1}{2}LI_{0}^{2}=\frac{1}{2}C{{u}^{2}}+\frac{1}{2}L{{i}^{2}}\)

\(\Rightarrow {{I}_{0}}=\sqrt{\frac{C{{u}^{2}}-L{{i}^{2}}}{L}}=...=0,05\text{ }A\)

→ Chọn đáp án A

Ví dụ 7: Điện tích cực đại của tụ trong mạch LC có tần số riêng \(f={{10}^{5}}Hz\) là \({{q}_{0}}={{6.10}^{-9}}C\). Khi điện tích của tụ là \(q={{3.10}^{-9}}C\) thì dòng điện trong mạch có độ lớn:

A. \(6\sqrt{3}\pi {{.10}^{-4}}A\)                       

B. \(6\pi {{.10}^{-4}}A\)            

C. \(6\sqrt{2}\pi {{.10}^{-4}}A\)                              

D. \(2\sqrt{3}\pi {{.10}^{-5}}A\)

Hướng dẫn giải

Ta có: \(\frac{Q_{0}^{2}}{2.C}=\frac{{{q}^{2}}}{2.C}+\frac{1}{2}.L{{i}^{2}}\Rightarrow Q_{0}^{2}-{{q}^{2}}=LC.{{i}^{2}}=\frac{{{i}^{2}}}{{{\omega }^{2}}}\Rightarrow {{i}^{2}}={{\omega }^{2}}\left( Q_{0}^{2}-{{q}^{2}} \right)\Rightarrow i=\omega \sqrt{Q_{0}^{2}-{{q}^{2}}}\)

Thay vào ta tính được \(i=6\sqrt{3}\pi {{.10}^{-4}}A\)

→ Chọn đáp án A

Bài 1: Công thức tính năng lượng điện từ của mạch dao động LC là           

A. \(W=\frac{Q_{0}^{2}}{2L}\)                        

B. \(W=\frac{Q_{0}^{2}}{2C}\)         

C. \(W=\frac{Q_{0}^{2}}{C}\)                                

D. \(W=\frac{Q_{0}^{2}}{L}\)

Bài 2: Biểu thức nào liên quan đến dao động điện từ sau đây là không đúng ?

A. Năng lượng từ trường tức thời: \({{W}_{L}}=\frac{L{{i}^{2}}}{2}\)

B. Năng lượng điện trường tức thời \({{W}_{C}}=\frac{C{{u}^{2}}}{2}\)

C. Tần số của dao động điện từ tự do là \(f=\frac{1}{2\pi \sqrt{LC}}\)

D. Tần số góc của dao động điện từ tự do là \(\omega =\sqrt{LC}\)

Bài 3: Trong mạch dao động LC có điện trở thuần bằng không thì

A. Năng lượng điện trường tập trung ở cuộn cảm và biến thiên với chu kỳ bằng chu kỳ dao động riêng của mạch.

B. Năng lượng từ trường tập trung ở tụ điện và biến thiên với chu kỳ bằng nửa chu kỳ dao động riêng của mạch.

C. Năng lượng từ trường tập trung ở cuộn cảm và biến thiên với chu kỳ bằng chu kỳ dao động riêng của mạch.                                

D. Năng lượng điện trường tập trung ở tụ điện và biến thiên với chu kỳ bằng nửa chu kỳ dao động riêng của mạch.

Bài 4: Trong một mạch dao động điện từ LC, điện tích của tụ biến thiên theo hàm số \(q={{Q}_{0}}sin\left( \pi t \right)\text{ C}\). Khi điện tích của tụ điện là \(q=\frac{{{Q}_{0}}}{\sqrt{2}}\) thì năng lượng điện trường

A. bằng năng lượng từ trường                              

B. bằng hai lần năng lượng từ trường   

C. bằng ba lần năng lượng từ trường                   

D. bằng một nửa năng lượng từ trường

Bài 5: Trong một mạch dao động điện từ LC, điện tích của tụ biến thiên theo hàm số \(q={{Q}_{0}}\cos \left( \pi t \right)\text{ }C\). Khi điện tích của tụ điện là \(q=\frac{{{Q}_{0}}}{2}\) thì năng lượng từ trường

A. bằng bốn lần năng lượng điện trường             

B. bằng năng lượng từ trường

C. bằng ba lần năng lượng điện trường               

D. bằng hai lần năng lượng điện trường

Bài 6: Cường độ dòng điện trong mạch dao động lí tưởng biến đổi với tần số f. Phát biểu nào sau đây là không đúng ?

A. Năng lượng điện từ không biến đổi.                

B. Năng lượng điện từ biến đổi với tần sổ f/2.

C. Năng lượng từ trường biến đổi với tần số 2f.

 D. Năng lượng điện trường biến đổi với tần số 2f.

Bài 7: Nhận xét nào sau đây liên quan đến năng lượng điện từ của mạch dao động là đúng? Điện tích trong mạch dao động lí tưởng biến đổi với chu kỳ T thì

A. Năng lượng điện trường biến đổi với chu kỳ T/2.

B. Năng lượng điện trường biến đổi với chu kỳ 2T.                                  

C. Năng lượng từ trường biến đổi với chu kỳ 2T.

D. Năng lượng điện từ biến đổi với chu kỳ T/2.

Bài 8: Xét mạch dao động lí tưởng LC. Khoảng thời gian ngắn nhất kể từ lúc năng lượng điện trường cực đại đến lúc năng lượng từ trường cực đại là

A. \(\Delta t=2\pi \sqrt{LC}\)                               

B. \(\Delta t=\frac{\pi \sqrt{LC}}{4}\) 

C. \(\Delta t=\pi \sqrt{LC}\)                       

D. \(\Delta t=\frac{\pi \sqrt{LC}}{2}\)

Bài 9: Trong mạch điện dao động điện từ LC, hiệu điện thế trên tu tai thời điểm \({{\text{W}}_{d}}=\frac{1}{n}{{\text{W}}_{t}}\) được tính theo biểu thức:

A. \(u=\frac{{{U}_{0}}}{2}\sqrt{n+1}\)           

B. \(u=2{{U}_{0}}\sqrt{n+1}\)

C. \(u=\frac{{{U}_{0}}}{\sqrt{n+1}}\)                   

D. \(u=\frac{{{U}_{0}}}{\omega }\sqrt{n+1}\)

Bài 10: Nhận xét nào sau đây liên quan đến năng lượng điện từ của mạch dao động là sai ?

A. Tại mọi thời điểm, tổng năng lượng điện trường và năng lượng từ trường là không đổi.

B. Năng lượng điện trường và năng lượng từ trường biến đổi tuần hoàn với chu kỳ T/2.

C. Năng lượng điện trường và năng lượng từ trường biến đổi tuần hoàn không theo một tần số chung.   

D. Năng lượng của mạch dao động gồm năng lượng điện trường tập trung ở tụ điện và năng lượng từ trường tập trung ở cuộn cảm.

-----( Để xem đầy đủ nội dung của tài liệu, các em vui lòng xem Online hoặc Đăng nhập để tải về máy)------

ĐÁP ÁN PHẦN LUYỆN TẬP

1B	2D	3D	4A	5C	6B	7A	8D	9C	10C
11B	12A	13A	14C	15C	16D	17C	18D	19A	20B
21C	22C	23C	24C	25B	26D	27C	28D	29A	30C

 

Trên đây là trích dẫn một phần nội dung tài liệu Phương pháp giải bài tập về năng lượng trong mạch dao động LC môn Vật Lý 12 năm 2021-2022. Để xem thêm nhiều tư liệu hữu ích khác, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.