Giải Lý 12 SGK nâng cao Chương 2 Bài 6 Dao động điều hòa

Tốc độ của chất điểm dao động điều hòa cực đại khi:

    A. Li độ cực đại      B. gia tốc cực đại

    C. li độ bằng 0      D. pha bằng \(\frac{\pi }{4}\)

Hướng dẫn giải:

Tốc độ của chất điểm dao động điều hòa cực đại khi li độ bằng 0 

Chọn đáp án C

---

Gia tốc của chất điểm dao động điều hòa bằng 0 khi:

   A. Li độ cực đại

   B. Li độ cực tiểu

   C. Vận tốc cực đại hoặc cực tiểu

   D. Vận tốc bằng 0.

Hướng dẫn giải:

Gia tốc của chất điểm dao động điều hòa bằng 0 khi vận tốc cực đại hoặc cực tiểu

Chọn đáp án C

---

Dao động cơ điều hòa đổi chiều khi:

   A. Lực tác dụng đổi chiều

   B. Lực tác dụng bằng 0

   C. Lực tác dụng có độ lớn cực đại

   D. Lực tác dụng có độ lớn cực tiểu.

Hướng dẫn giải:

Dao động cơ điều hòa đổi chiều khi lực tác dụng có độ lớn cực đại

Chọn đáp án C

---

a) Thử lại rằng: \(x = {A_1}\cos \omega t + {A_2}\sin \omega t\)  (6.14) trong đó A₁ và A₂ là hai hằng số bất kì cũng là nghiệm của phương trình (6.3).

b) Chứng tỏ rằng, nếu chọn A1 và A2 trong  biểu thức ở vế trái của (6.14) như sau:  \({A_1} = A\cos \varphi ;{A_2} =  - A\sin \varphi \) thì biểu thức ấy trùng với biểu thức ở vế phải của (6.4).

Hướng dẫn giải:

a) Ta có: 

\(\begin{array}{l}
x = {A_1}\cos \omega t + {A_2}\sin \omega t\\
 \Rightarrow x' =  - {A_1}\omega \sin \omega t + {A_2}\omega \cos \omega t.\\
x =  - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}\sin \omega t.
\end{array}\)

Ta thu được:

\(\begin{array}{l}
x + {\omega ^2}x =  - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}sin\omega t + {\omega ^2}({A_1}\cos \omega t + {A_2}\sin \omega t)\\
 \Rightarrow x + {\omega ^2}x =  - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}sin\omega t + {A_1}{\omega ^2}\cos \omega t + {A_2}{\omega ^2}sin\omega t = 0
\end{array}\)

Vậy :  \(x = {A_1}\cos \omega t + {A_2}\sin \omega t\) là nghiệm của phương trình \(x + {\omega ^2}x = 0.\)

b) Nếu ta chọn \({A_1} = A\cos \varphi \) và \({A_2} =  - A\sin \varphi \)

thì :

\(\begin{array}{l}
x = {A_1}\cos \omega t + {A_2}\sin \omega t\\
 = A\cos \varphi cos\omega t - A\sin \varphi \sin \omega t\\
 = A(\cos \varphi cos\omega t - \sin \varphi \sin \omega t)\\
 \Rightarrow x = Acos\left( {\omega t + \varphi } \right).
\end{array}\)

---

Phương trình dao động của một vật là: \(x = 6cos(4\pi t + \pi 6)(cm).\)

a) Xác định biên độ, tần số góc, chu kì tần số của dao động.

b) Xác định pha dao động tại thời điểm \(t=14s\), từ đó suy ra li độ tại thời điểm ấy.

c) Vẽ vectơ quay biểu diễn dao động vào thời điểm \(t=0\).

Hướng dẫn giải:

Phương trình dao động của vật: \(x = 6cos(4\pi t + \pi 6)(cm).\)$$

a) Biên độ \(A=6\) (cm)

Chu kì : \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5(s)\)

Tần só góc : \(\omega  = 4\pi (rad/s)\)

Tần số : \(f = \frac{1}{T} = \frac{1}{{0,5}} = 2(Hz)\)

b) Khi  \(t = \frac{1}{4}(s) \Rightarrow pha\:(\omega t + \varphi ) = \left( {4\pi .\frac{1}{4} + \frac{\pi }{6}} \right) = \frac{{7\pi }}{6}\)

\( \Rightarrow x = 6\cos \left( {\pi  + \frac{\pi }{6}} \right) =  - 6\cos \frac{\pi }{6} =  - 6.\frac{{\sqrt 3 }}{2}\)

\(( =  - 3\sqrt 3 (cm).\)

c) Vẽ vectơ quay biểu diễn dao động vào thời điểm \(t=0\):

---

Một vật dao động điều hòa với biên độ A = -4 cm và chu kì T = 2s.

    a) Viết phương trình dao động của vật, chọn gốc thời gian là lúc nó đi qua vị trí cân bằng theo chiều dương.

    b) Tính li độ của vật tại thười điểm t = 5,5s.

Hướng dẫn giải:

Dạng tổng quát của phương trình dao động là x = Acos(ωt + φ)

Ta có:

Biên độ A = 4cm; Tần số góc: ω = 2π/T = π (rad/s)$$

Chọn gốc thời gian lúc vật qua vị trí cân bằng theo chiều dương

⇒ Khi \(t=0\), ta có: \(\begin{array}{l}
{x_0} = Acos\varphi  = 0\,(1)\\
{v_0} =  - A\omega sin\varphi  > 0\,(2)
\end{array}\)

Từ \({(1) \Rightarrow cos\varphi  = 0}\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}
{\varphi  = \frac{\pi }{2}}\\
{\varphi  =  - \frac{\pi }{2}}
\end{array}} \right.\)

Từ \({(2) \Rightarrow {v_0} > 0 \Leftrightarrow sin\varphi  < 0}\)

\({ \to \varphi  =  - \frac{\pi }{2}.}\)

Vậy : \(x = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)(cm).\)

b) Khi \(t=5,5\) (s), ta có

\(\begin{array}{l}
x = 4cos(\pi .5,5 - \frac{\pi }{2})\\
x = 4cos5\pi  =  - 4(cm)
\end{array}\)

---

Một vật nặng treo vào lò xo làm cho lò xo dãn ra 0,8 cm. Cho vật dao động. Tìm chu kì dao động ấy. Lấy g = 10 m/s².

Hướng dẫn giải:

Khi treo vật vào lò xo làm lò xo dãn ra một đoạn \({\rm{\Delta }}\ell  = 0,8(cm)\) ở vị trí cân bằng.

Theo định luật I Niutơn:

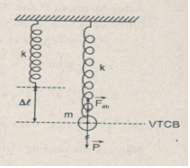
\(\begin{array}{l}
\vec P + \overrightarrow {{F_{dh}}}  = 0\\
 \Leftrightarrow P = {F_{dh}}\\
 \Leftrightarrow mg = k{\rm{\Delta }}\ell \\
 \Leftrightarrow \frac{m}{k} = \frac{{{\rm{\Delta }}\ell }}{g}
\end{array}\)

Khi cho vật dao động, chu kì dao động của con lắc lò xo là: 

\(T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{{\rm{\Delta }}\ell }}{g}}  = 2\pi \sqrt {\frac{{0,{{8.10}^{ - 2}}}}{{10}}}  = 0,18(s)\)

 

Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Vật lý 12 Chương 2 Bài 6 Dao động điều hòa được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 học tập thật tốt!