Mời các em cùng tham khảo Đề thi thử tốt nghiệp THPT môn Toán 12 năm 2022-2023 có đáp án Sở GD&ĐT Hà Tĩnh do HOC247 sưu tầm và biên soạn nhằm giúp cho các em học sinh lớp 12 trong quá trình ôn thi để học tập chủ động hơn, nắm bắt các kiến thức tổng quan về môn học và chuẩn bị tốt cho kì thi tốt nghiệp sắp tới. Hi vọng tài liệu này sẽ là người bạn đồng hành, giúp các em đạt kết quả cao trong học tập.
|
SỞ GD&ĐT HÀ TĨNH ONLINE LẦN THỨ NHẤT (Đề thi có 5 trang, 50 câu)
|
KỲ THI THỬ TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2023 Môn: TOÁN Thời gian làm bài 90 phút, không kể thời gian phát đề |
|
MÃ ĐỀ: 001 |
Họ, tên thí sinh: ……………………………………………………
Số báo danh: ……………………………………………………….
1. Đề thi
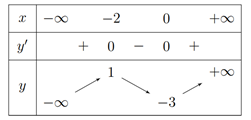
Câu 1: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Hàm số nghịch biến trên khoảng nào dưới đây?
A. \(\left( {1; - 3} \right).\)
B. \(\left( { - \infty ; - 2} \right).\)
C. \(\left( { - 2;0} \right).\)
D. \(\left( { - 3;1} \right).\)
Câu 2: Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong hình bên. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng
.png)
A. (0;2)
B. (1;2)
C. \((-\infty;1) \)
D. \((2;+\infty)\)
Câu 3: Cho hàm số \(y = \frac{{x + 3}}{{x + 1}}.\) Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên R.
D. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;+ \infty} \right)\)
Câu 4: Hàm số nào sau đây đồng biến trên khoảng \(\left( { - \infty ;+ \infty} \right)\)
A. \( y=-x^3-3x\) .
B. \(y = \frac{{x + 1}}{{x + 3}}.\) .
C. \(y = \frac{{x - 1}}{{x - 2}}.\).
D. \(y=x^3+3x\).
Câu 5: Hàm số \( y=x^4+x^2-2\) nghịch biến trên khoảng nào trong các khoảng sau?
A. \((-\infty;0) \) .
B. \((-2;1)\).
C. \((0;+\infty)\).
D. \((0;2)\).
Câu 6: Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của hàm số \(y = f'\left( x \right)\) như hình dưới đây.

Số điểm cực trị của hàm số bằng
A. 2.
B. 5.
C. 1.
D. 0.
Câu 7: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 34 học sinh?
A. \( 2^3\).
B. \( A_{34}^2\)
C. \({34^2} \) .
D. \(C_{34}^2\).
Câu 8: Cho hàm số \(y=\frac{2x+1}{x-1}.\) Điểm nào sau đây thuộc đồ thị hàm số?
A. \(\left( 0;1 \right)\).
B. \(\left( 2;-5 \right)\).
C. \(\left( 0;-1 \right)\).
D. \(\left( 1;3 \right)\).
Câu 9: Cho cấp số nhân \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=5\) và công bộ \(q=2.\) Giá trị \({{u}_{2}}\) bằng
A. 25.
B. 10.
C. \(\frac{5}{2}\). .
D. 32.
Câu 10: Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hàm số đã cho có bao nhiêu điểm cực trị?

A. 1.
B. 0.
C. 2.
D. 4.
Câu 11: Điểm nào sau đây là điểm cực tiểu của đồ thị hàm số \(y={{x}^{3}}-3x+1\)?
A. \(\left( -1;1 \right)\).
B. \(\left( -1;3 \right)\).
C. \(\left( 1;3 \right)\).
D. \(\left( 1;-1 \right)\).
Câu 12: Hàm số \(y={{x}^{3}}+2\). có bao nhiêu điểm cực trị?
A. 1.
B. 0.
C. 2.
D. 3.
Câu 13: Giá trị lớn nhất của hàm số \(f\left( x \right)={{x}^{3}}-3x\) trên đoạn \(\left[ -3;3 \right]\) bằng
A. -18.
B. 18.
C. 2
D. -2.
Câu 14: Tiệm cận đứng của đồ thị hàm số \(y=\frac{x+1}{x+3}\) bằng
A. \(x=-3\).
B. \(x=-1\).
C. \(x=1\).
D. \(x=3\).
Câu 15: Cho hàm số \(y=f\left( x \right)\) có tập xác định \(R\backslash \left\{ -1 \right\},\) có bảng biến thiên như hình vẽ. Đồ thị hàm số có tất cả bao nhiêu tiệm cân đứng và tiệm cận ngang?
.png)
A. 4.
B. 1.
C. 2.
D. 3.
Câu 16: Đồ thị hàm số \(y=\frac{{{x}^{2}}-5x+4}{x-2}\) cắt trục hoành tại bao nhiêu điểm?
A. 1.
B. 2.
C. 3.
D. 0.
Câu 17: Thể tích của khối lăng trụ có chiều cao bằng \(h\) và diện tích đáy bằng \(B\) là
A. \(V=Bh\).
B. \(V=\frac{1}{3}Bh\).
C. \(V=\frac{1}{6}Bh\).
D. \(V=\frac{1}{2}Bh\).
Câu 18: Một hình chóp có chiều cao bằng 10cm và diện tích đáy \(30c{{m}^{2}}\) thì có thể tích bằng
A. \(300c{{m}^{3}}\).
B. \(1000\sqrt{2}c{{m}^{3}}\).
C. \(100c{{m}^{3}}\).
D. \(900c{{m}^{3}}\).
Câu 19: Giá trị nhỏ nhất của hàm số \(y=\frac{3x+1}{x-2}\) trên \(\left[ -1;1 \right]\) bằng
A. \(-4\).
B. \(\frac{2}{3}\).
C. \(4\).
D. \(-\frac{2}{3}\).
Câu 20: Cho khối chóp \(S.ABCD\) có đáy \(ABCD\). là hình vuông cạnh bằng \(a,\) cạnh bên \(SA\). vuông góc với mặt đáy và \(SA=3a.\) Thể tích của khối chóp \(S.ABCD\) bằng
A. \(\frac{1}{3}{{a}^{3}}\).
B. \(3{{a}^{3}}\).
C. \({{a}^{3}}.\)
D. \(9{{a}^{3}}\).
Câu 21: Hình đa diện bên có tất cả bao nhiêu mặt?
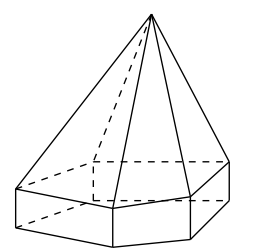
A. 11.
B. 20.
C. 12.
D. 10.
Câu 22: Cho hàm số có bảng biến thiên như hình vẽ bên. Đặt \(\mathop {\min }\limits_{x \in \left[ { - 2;2} \right]}\,f\left( x \right)=m,\mathop {\max}\limits_{x \in \left[ { - 2;2} \right]}\,f\left( x \right)=M.\) Khẳng định nào dưới đây đúng?
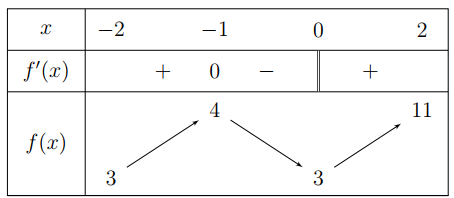
A. \(m=-2;M=-1\).
B. \(m=3;M=4\).
C. \(m=-2;M=2\).
D. \(m=3;M=11\). \[ \]
Câu 23: Cho hàm số \(y=f\left( x \right)\) có \(\underset{x\to +\infty }{\mathop{\lim }}\,y=1\) và \(\underset{x\to -\infty }{\mathop{\lim }}\,y=-1.\) Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng \(x=1\) và \(x=-1\).
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng \(y=1\) và \(y=-1\).
C. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Câu 24: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau. Mệnh đề nào sau đây SAI?
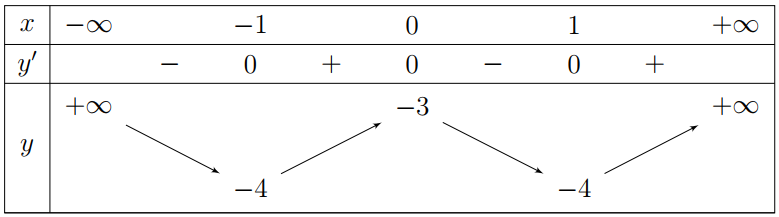
A. Hàm số đồng biến các khoảng \(\left( -1;0 \right)\) và \(\left( 1;+\infty \right)\).
B. Hàm số đạt cực đại tại \(x=0\).
C. Hàm số có giá trị nhỏ nhất bằng \(-4\).
D. Hàm số có giá trị lớn nhất bằng \(-3\).
Câu 25: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
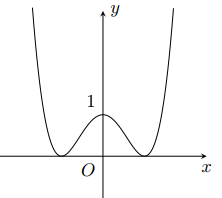
A. \(y={{x}^{4}}-2x+1\).
B. \(y=-{{x}^{4}}+2{{x}^{2}}+1\).
C. \(y={{x}^{4}}-2{{x}^{2}}-1\).
D. \(y={{x}^{4}}-2{{x}^{2}}+1\).
Câu 26: Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị trong hình bên. Số nghiệm của phương trình \(f\left( x \right)=1\) là
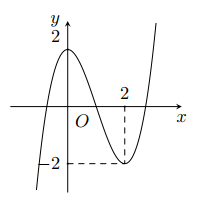
A. 0.
B. 2.
C. 3.
D. 1.
Câu 27: Giá trị cực tiểu của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+2\) là.
A. 3.
B. \(-25\).
C. 7.
D. \(-20\).
Câu 28: Đường thẳng \(y=2x+1\) cắt đồ thị hàm số \(y={{x}^{3}}+3{{x}^{2}}+4x-5\) tại
A. bốn điểm.
B. hai điểm.
C. một điểm.
D. ba điểm.
Câu 29: Diện tích ba mặt của hình hộp chữ nhật lần lượt là \(15c{{m}^{2}},24c{{m}^{2}},40c{{m}^{2}}.\) Thể tích của khối hộp đó là
A. \(150c{{m}^{3}}\)
B. \(140c{{m}^{3}}\)
C. \(100c{{m}^{3}}\)
D. \(120c{{m}^{3}}\)
Câu 30: Cho hàm số \(y=-2{{x}^{3}}+6{{x}^{2}}-5\) có đồ thị \(\left( C \right).\) Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) có hoành độ bằng 3 là
A. \(y=18x+49\).
B. \(y=-18x-49\).
C. \(y=-18x+49\).
D. \(y=18x-49\).
Câu 31: Cho hàm số \(f\left( x \right)=\left\{ \begin{align}
& -{{x}^{2}}+2x\text{ voi }x<1 \\
& -2x+3x\text{ voi }x\ge 1 \\
\end{align} \right.\). Tìm giá trị nhỏ nhất \(m\) của hàm số trên đoạn \(\left[ -1;2 \right].\)
A. \(m=-1\).
B. \(m=-3\).
C. \(m=1\).
D. \(m=-2\).
Câu 32: Tính thể tích \(V\) của khối lăng trụ tam giác đều có tất cả các cạnh bằng \(a.\)
A. \(V=\frac{\sqrt{2}{{a}^{3}}}{3}\).
B. \(V=\frac{\sqrt{3}{{a}^{3}}}{4}\).
C. \(V=\frac{\sqrt{2}{{a}^{3}}}{4}\).
D. \(V=\frac{\sqrt{3}{{a}^{3}}}{2}\).
Câu 33: Cho khối chóp \(S.ABC\). Gọi \(M,N\) lần lượt là trung điểm \(SA\) và \(SB.\) Tính tỉ số thể tích của hai khối chóp \(S.MNC\) và \(S.ABC\).
A. \(\frac{1}{4}\).
B. \(\frac{1}{2}\).
C. \(\frac{1}{3}\).
D. \(\frac{1}{8}\).
Câu 34: Cho khối chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng \(2a,\) mặt bên \(SAB\) vuông góc với mặt đáy. Tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( SAB \right).\)
A. \(a\sqrt{3}\).
B. \(\frac{a\sqrt{3}}{2}\).
C. \(2a\sqrt{3}\).
D. \(a\).
Câu 35: Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) và mặt bên \(ABB'A'\) là hình vuông cạnh bằng \(a\) (tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng \(BC'\) và mặt phẳng \(\left( ABB'A' \right).\)
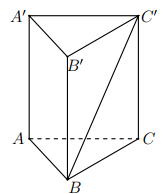
A. \(\frac{\sqrt{2}}{2}\).
B. \(\frac{\sqrt{6}}{3}\).
C. \(\frac{\sqrt{3}}{3}\).
D. \(\sqrt{2}.\)
Câu 36: Cho hàm số \(y={{x}^{3}}-m{{x}^{2}}+2x+1\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để hàm số đồng biến trên tập số thực \(R\)?
A. 7.
B. 6.
C. 5.
D. 4.
Câu 37: Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích bằng 48. Gọi \(M\) là trung điểm của cạnh \(AB.\) Tính thể tích \(V\) của khối tứ diện \(SMCD.\)
A. \(V=24\).
B. \(V=12\).
C. \(V=16.\)
D. \(V=36.\)
Câu 38: Cho hàm số \(y=\frac{x+1}{x-m},\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( 2;+\infty \right)?\)
A. 3.
B. 4.
C. 1.
D. 2.
Câu 39: Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(C,AB=a\sqrt{3},AC=2,SC=a\sqrt{5}.\) Hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAC \right)\) cùng vuông góc với mặt phẳng \(\left( ABC \right).\) Thể tích của khối chóp \(S.ABC\) bằng
A. \(\frac{2\sqrt{2}{{a}^{3}}}{3}\).
B. \(\frac{\sqrt{6}{{a}^{3}}}{4}\).
C. \(\frac{\sqrt{2}{{a}^{3}}}{3}\).
D. \(\frac{\sqrt{10}{{a}^{3}}}{6}\).
Câu 40: Một hộp chứ 7 viên bi đỏ, 8 viên bi trắng, 6 viên bi vàng. Lấy ngẫu nhiên trong hộp ra 4 viên bi. Tính xác suất để chọn được 4 viên bi trong đó có nhiều nhất 2 viên bi vàng.
A. \(\frac{13}{14}\).
B. \(\frac{12}{13}\).
C. \(\frac{18}{19}\).
D. \(\frac{15}{16}\).
Câu 41: Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ. Xét dấu của \(a,b,c.\)
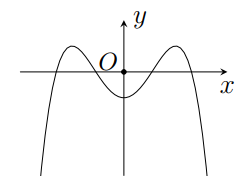
A. \(a<0,b<0,c<0\).
B. \(a>0,b<0,c<0\).
C. \(a<0,b>0,c<0\).
D. \(a<0,b<0,c>0\).
Câu 42: Biết rằng giá trị nhỏ nhất của hàm số \(y=mx+\frac{36}{x+1}\) trên \(\left[ 0;3 \right]\) bằng 20. Mệnh đề nào sau đây đúng?
A. \(4 < m\le 8 \)
B. \(0 < m\le 2\)
C. \(2 < m\le 4\)
D. \(m>8\).
Câu 43: Cho hàm bậc ba \(f\left( x \right)\) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(g\left( x \right)=\frac{1}{f\left( x \right)-2}\) là
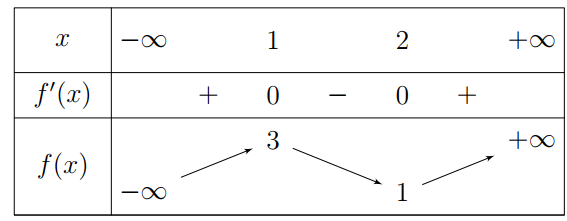
A. 2.
B. 4.
C. 1.
D. 3.
Câu 44: Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng \(200{{m}^{3}}\) đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công cây bể là 300.000 đồng/\({{m}^{2}}\). Chi phí xây dựng thấp nhất là
A. 51 triệu đồng.
B. 75 triệu đồng.
C. 46 triệu đồng.
D. 36 triệu đồng.
Câu 45: Một chất điểm chuyển động theo quy luật \(s\left( t \right)={{t}^{2}}-\frac{1}{6}{{t}^{3}}\left( m \right).\) Tìm thời điểm \(t\) (giây) mà tạo đó vận tốc \(v\left( m/s \right)\) của chuyển động đạt giá trị lớn nhất.
A. \(t=2\).
B. \(t=0,5\).
C. \(t=2,5\).
D. \(t=1\).
Câu 46: Cho hàm số \(y=f\left( x \right).\) Hàm số \(y=f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right)=f\left( {{x}^{3}}+1 \right)\) nghịch biến trên khoảng
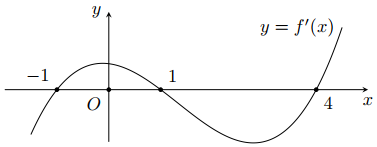
A. \(\left( -\infty ;-2 \right)\).
B. \(\left( -\infty ;\sqrt[3]{3} \right).\)
C. \(\left( -\infty ;-1 \right)\).
D. \(\left( 0;\frac{3}{2} \right)\).
Câu 47: Cho lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có \(AC=4a.\) Gọi \(O\) là tâm của mặt \(A'B'C'D'.\) Biết rằng hai mặt phẳng \(\left( OAB \right)\) và \(\left( OCD \right)\) vuông góc với nhau. Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng
A. \(\frac{16{{a}^{3}}\sqrt{2}}{3}\).
B. \(\frac{8{{a}^{3}}\sqrt{2}}{3}\).
C. \(16{{a}^{3}}\)
D. \(8{{a}^{3}}\sqrt{2}\)
Câu 48: Cho khối chóp \(S.ABC\) có \(AB\bot BC,BC\bot SC,SC\bot SA,BC=a,SC=\sqrt{15}a\) và góc giữa \(AB,SC\) bằng \({{30}^{0}}.\) Thể tích khối chóp \(S.ABC\) bằng
A. \(\frac{5\sqrt{3}{{a}^{3}}}{2}\).
B. \(\frac{5}{6}{{a}^{3}}\).
C. \(\frac{5{{a}^{3}}}{2}\).
D. \(\frac{5\sqrt{3}{{a}^{3}}}{6}\).
Câu 49: Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( \sqrt[3]{f\left( x \right)+m} \right)={{x}^{3}}-m\) có nghiệm \(x\in \left[ 1;2 \right]\) biết \(f\left( x \right)={{x}^{5}}+3{{x}^{3}}-4m.\)
A. 24.
B. 64.
C. 15.
D. 16.
Câu 50: Cho hàm số \(y=f\left( x \right)\) liên tục trên \(R,\) có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số
\(g\left( x \right)=\left| f\left( \left| 6x-5 \right| \right)+2021+m \right|\)
Có 3 điểm cực đại?
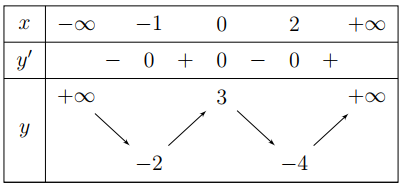
A. 5.
B. 6.
C. 7.
D. 8.
----- HẾT -----
2. Đáp án và hướng dẫn giải
HƯỚNG DẪN GIẢI CHI TIẾT
|
1-C |
2-D |
3-D |
4-D |
5-A |
6-A |
7-D |
8-C |
9-B |
10-C |
|
11-D |
12-B |
13-B |
14-A |
15-C |
16-B |
17-A |
18-C |
19-A |
20-C |
|
21-A |
22-D |
23-B |
24-D |
25-D |
26-C |
27-B |
28-C |
29-D |
30-C |
|
31-B |
32-B |
33-A |
34-A |
35-A |
36-A |
37-A |
38-A |
39-C |
40-C |
|
41-C |
42-C |
43-B |
44-A |
45-A |
46-A |
47-D |
48-C |
49-D |
50-B |
Câu 1:
Từ bảng biến thiên dễ thấy hàm số nghịch biến trên khoảng \(\left( -2;0 \right).\)
Chọn đáp án C.
Câu 2:
Dựa vào đồ thị, ta thấy hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( 2;+\infty \right).\)
Chọn đáp án D.
Câu 3:
Điều kiện xác định \(x\in \left( -\infty ;-1 \right)\cup \left( -1;+\infty \right).\)
\(y'=-\frac{2}{{{\left( x+1 \right)}^{2}}}<0\) với mọi \(x\in \left( -\infty ;-1 \right)\cup \left( -1;+\infty \right).\)
Vậy hàm số nghịch biến trên khoảng \(\left( -\infty ;-1 \right).\)
Chọn đáp án D.
Câu 4:
* Hàm số \(y=\frac{x-1}{x-2}\) có tập xác định \(D=\mathbb{R}\backslash \left\{ 2 \right\}\) nên hàm số không thể đồng biến trên khoảng \(\left( -\infty ;+\infty \right)\).
* Hàm số \(y=-{{x}^{3}}-3x\) có \(y'=-3{{x}^{2}}-3<0,\forall x\in \mathbb{R}\) nên hàm số nghịch biến trên khoảng \(\left( -\infty ;+\infty \right).\)
* Hàm số \(y=\frac{x+1}{x+3}\) có tập xác định \(D=\mathbb{R}\backslash \left\{ -3 \right\}\) nên hàm số không thể đồng biến trên khoảng \(\left( -\infty ;+\infty \right).\)
Vậy đáp án đúng là \(y={{x}^{3}}+x.\)
Chọn đáp án D.
Câu 5:
Tập xác định \(D=\mathbb{R}.\) Ta có \(y'=4{{x}^{3}}+2x=2x\left( 2{{x}^{2}}+1 \right)\).
Ta có \(y'>0,\forall x>0\) và \(y'<0,\forall x<0.\) Suy ra hàm số nghịch biến trên khoảng \(\left( -\infty ;0 \right).\)
Chọn đáp án A.
---(Để xem tiếp nội dung của hướng dẫn giải các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
------ HẾT ------
Trên đây là toàn bộ nội dung Đề thi thử tốt nghiệp THPT môn Toán 12 năm 2022-2023 có đáp án Sở GD&ĐT Hà Tĩnh. Để xem toàn bộ hướng dẫn giải các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.