Nội dung tài liệu Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Tân Lập được biên soạn bởi HOC247 sau đây giúp các em học sinh lớp 10 ôn tập và rèn luyện kĩ năng giải đề, chuẩn bị cho kì thi vào lớp 10. Hi vọng với tài liệu, các em sẽ ôn tập kiến thức dễ dàng hơn. Chúc các em học tập tốt!
|
TRƯỜNG THCS TÂN LẬP |
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2022 – 2023 Thời gian: 120 phút |
ĐỀ SỐ 1
Câu 1.(1,5 điểm). Cho \(\left( P \right):y=\frac{1}{2}{{x}^{2}}\) và đường thẳng \(\left( d \right):y=x+4\) .
a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình \({{x}^{2}}+5x-7=0\) có 2 nghiệm là \({{x}_{1}},{{x}_{2}}\) . Không giải phương trình, hãy tính giá trị của biểu thức \(A=x_{1}^{2}+x_{2}^{2}-2{{x}_{1}}{{x}_{2}}\)
Câu 3.(1 điểm). Ở trường A, đầu năm học số học sinh nam và nữ bằng nhau. Cuối học kỳ I, trường nhận thêm 15 học sinh nữ và 5 học sinh nam nên số học sinh nữ lúc này chiếm 51% tổng số học sinh. Hỏi đầu năm học trường đó có bao nhiêu học sinh?
Câu 4.(0,75 điểm). Giá bán 1 cái tivi giảm giá 2 lần, mỗi lần 10% so với giá đang bán, sau khi giảm giá 2 lần đó thì giá còn lại là 12150000 đồng. Hỏi nếu ngay từ đầu cũng giảm giá 2 lần, mỗi lần chỉ giảm giá 5% so với giá đang bán thì sau khi giảm giá 2 lần đó thì giá tivi này còn lại bao nhiêu tiền?
Câu 5.(1 điểm). Công ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản phẩm) là số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y=ax+b(a,b là hằng số). Biết với giá bán là 400000( đồng)/sản phẩm thì số lượng sản phẩm bán ra là 1200 (sản phẩm); với giá bán là 460000 (đồng)/sản phẩm thì số lượng sản phẩm bán ra là 1800 (sản phẩm).
a) Xác định a, b.
b) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 440000 đồng.
Câu 6.(1 điểm). Để chứa xăng hoặc dầu, người ta chế tạo ra các thùng phuy bằng sắt (hình vẽ) dạng hình trụ có 2 đáy là hình tròn có đường kính \(560\text{m}m\).
a) Tính diện tích của một mặt đáy của thùng phuy?(Làm tròn kết quả đến \(d{{m}^{2}}\))
b) Biết thùng phuy chứa được khoảng 200 lít dầu. Tính chiều cao h của thùng phuy và diện tích sắt để làm thùng phuy, giả thiết diện tích các chỗ hàn không đáng kể? (Làm tròn kết quả đến \(d{{m}^{2}}\))
Câu 7.(1 điểm). Giả sử cách tính tiền nước sinh hoạt cho 1 người ở TP. Hồ Chí Minh như sau:
Mức 1 cho \(4{{\text{m}}^{3}}\) dầu tiên là 7000 đồng/ \({{m}^{3}}\);
Mức 2 cho \(3{{\text{m}}^{3}}\) tiếp theo là \(10000\) đồng/ \({{m}^{3}}\);
Mức 3 cho số ${{m}^{3}}$ còn lại là 12500 đồng/ \({{m}^{3}}\).
- Số tiền nước phải trả cho ba mức này gọi là A.
- Thuế VAT: B=A.10%.
- Thuế môi trường: C=A.15%.
Tổng số tiền phải trả là : T=A+B+C.
Tháng 9/2018 gia đình cô Bảy có 2 người phải trả hết số tiền: T=207500 đồng. Hỏi gia đình cô Bảy dùng hết bao nhiêu \({{m}^{3}}\) nước
Câu 8.(3 điểm) Cho \(\Delta ABC\) nội tiếp trong đường tròn (O,R) (dùng sai dấu ngoặc \(\left( O;\,R \right)\)). Ba đường cao AD,BE,CF cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BCEF nội tiếp.
b) Kẻ đường kính AK của (O). Chứng minh và \(AB\cdot AC=2R\cdot AD\).
c) Gọi M là trung điểm của BC,I là giao điểm EF và BC. Chứng minh tứ giác EFDM nội tiếp và \(IB\cdot IC=ID\cdot IM\)
ĐÁP ÁN
a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\):
\(\frac{1}{2}{{x}^{2}}=x+4\Leftrightarrow \frac{1}{2}{{x}^{2}}-x-4=0\Leftrightarrow x=-2;x=4\)
Thay x=-2 vào y=x+4, ta được: \(y=-2+4=2\).
Thay x=4 vào y=x+4, ta được: \(y=4+4=0\).
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(\left( -2;2 \right);\left( 4;8 \right)\)
---(Để xem tiếp nội dung của đề thi số 1 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 2
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS TÂN LẬP- ĐỀ 02
Câu 1.(1,5 điểm). Cho parabol \(\left( P \right):y={{x}^{2}}\) và đường thẳng \(\left( D \right):y=2x-1\).
a) Vẽ \(\left( P \right)\) và \(\left( D \right)\) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình \(3{{x}^{2}}-2x-2=0\) có 2 nghiệm là \({{x}_{1}},{{x}_{2}}\) . Không giải phương trình, hãy tính giá trị của biểu thức \(D=\frac{{{x}_{1}}}{{{x}_{2}}-1}+\frac{{{x}_{2}}}{{{x}_{1}}-1}\)
Câu 3.(0,75 điểm). Cách đây hơn 1 thế kỷ, nhà khoa học người Hà Lan Hendrich Lorentz đưa ra công thức tính số cân nặng lí tưởng của con người theo chiều cao như sau \(M=T-100-\frac{T-150}{N}\) (công thức Lorentz)
Trong đó : M là số cân nặng lí tưởng (kg), T là chiều cao (cm), N=4 với nam và N=2 với nữ
a) Bạn Huy (là nam) chiều cao 1,75m. Hỏi cân nặng của bạn nên là bao nhiêu kg để đạt lí tưởng (làm tròn kết quả đến kg)
b) Với chiều cao bằng bao nhiêu thì số cân nặng lí tưởng của nam giới và nữ giới bằng nhau? (làm tròn kết quả đến chữ số thập phân thứ nhất)
Câu 4.Ở các nước như Anh, Mỹ người ta thường tính nhiệt độ theo \({}^{0}F\) (Fahren-heit). Công thức để đổi từ \({}^{0}C\) sang \(^{0}F\) có dạng y=ax+b trong đó x là số chỉ \({}^{0}C\) và y là số chỉ của \({}^{0}F\) tương ứng. Biết rằng nhiệt độ của nước đá đang tan là \(({{0}^{0}}C)\) tương ứng với \({{32}^{0}}F\) và nhiệt độ của nước đang sôi \(({{100}^{0}}C)\) tương ứng với \({{212}^{0}}F\). Em hãy cho biết nhiệt độ của một người bình thường (\({{37}^{0}}C\)) sẽ là bao nhiêu \({}^{0}F\)?
Câu 5.( 1 điểm ). Cận thị trong học sinh ngày càng tăng. Lớp \(9\text{A}\) có 35 học sinh , trong đó chỉ có \(\frac{1}{4}\) số học sinh nam và \(\frac{1}{5}\) số học sinh nữ không bị cận thị. Biết tổng số học sinh nam và học sinh nữ không bị cân thị là 8. Tính số học sinh nữ không bị cận thị ?
Câu 6.( 1 điểm). Một người mua 3 đôi giày với hình thức khuyến mãi như sau : Nếu bạn mua một đôi giày với mức giá thông thường bạn sẽ nhận được giá giảm 30% khi mua đôi thứ hai và mua đôi thứ ba với nửa giá ban đầu. Bạn An đã trả tổng cộng là 1320000 đồng cho 3 đôi giày
a) Hỏi giá ban đầu của một đôi giày là bao nhiêu ?
b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 20% mỗi đôi giày. Hỏi bạn An nên chọn hình thức khuyến mãi nào nếu mua 3 đôi giày ?
Câu 7.(1 điểm). Một dụng cụ trộn bê tông gômg một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thuóc cho trên hình bên.
Hãy tính:
a) Thể tích của dụng cụ này.
b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy)
Câu 8.(3 điểm). Cho tam giác ABC nhọn (AB
a) Chứng minh : Tứ giác BKFC nội tiếp và \(MK\cdot MF=MB\cdot MC\)
b) AM cắt đường tròn (O) tại N \((N\ne A)\). Chứng minh \(\widehat{AKN}=\widehat{AFN}\)
c) Gọi I là hình chiếu của E lên AC. Tia EI cắt DC và đường tròn (O) lần lượt tại G và Q (\(Q\ne E\)). Chứng minh : I Là trung điểm của QG và 3 điểm N,F,Q thẳng hàng
---(Để xem tiếp nội dung của đề thi số 2 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 3
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS TÂN LẬP- ĐỀ 03
Câu 1.(1,5 điểm) Cho parabol \(\left( P \right):y=\frac{1}{2}{{x}^{2}}\) và đường thẳng \(\left( d \right):y=\frac{-1}{2}x+1\).
a) Vẽ \(\left( P \right)\) và \(\left( D \right)\) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) bằng phép toán.
Câu 2.(1,0 điểm) Cho phương trình: \(20{{x}^{2}}+5x-2020=0\) – 2020=0. Không giải phương trình trên, hãy tính giá trị của biểu thức sau: \(A=\frac{{{x}_{1}}}{{{x}_{2}}}\left( 1-{{x}_{2}} \right)+\frac{{{x}_{2}}}{{{x}_{1}}}\left( 1-{{x}_{1}} \right)\).
Câu 3.(1,0 điểm) Trong đợt dịch Covid - 19, học sinh hai lớp 9A và 9B trường THCS BK ủng hộ 212 chiếc khẩu trang cho những nơi cách li tập trung. Biết rằng số học sinh lớp 9A nhiều hơn số học sinh lớp 9B là 1 học sinh và mỗi học sinh lớp 9A ủng hộ 2 chiếc khẩu trang, mỗi học sinh lớp 9B ủng hộ 3 chiếc khẩu trang. Tìm số học sinh mỗi lớp.
Câu 4.(1,0 điểm) Nồng độ cồn trong máu \(\left( BAC \right)\) được định nghĩa là phần trăm rượu (rượu ethyl hoặc ethanol) trong dòng máu của một người. BAC 0,05% có nghĩa là có 0,05 gam rượu trong 100 ml máu. Càng uống nhiều rượu bia thì nồng độ cồn trong máu càng cao và càng nguy hiểm khi tham gia giao thông. Nồng độ BAC trong máu của một người được thể hiện qua đồ thị sau:
a) Viết công thức biểu thị mối quan hệ giữa nồng độ cồn trong máu \(\left( B \right)\) sau t giờ sử dụng.
b) Theo nghị định \(100/2019/N-CP\) về xử phạt vi phạm hành chính, các mức phạt (đối với xe máy).Hỏi sau 3 giờ, nếu người này tham gia giao thông thì sẽ bị xử phạt ở mức độ nào?
Câu 5.(1,0 điểm) Một siêu thị chạy chương trình khuyến mãi cho nước tăng lực có giá niêm yết là 9000 (đ/lon) như sau:
- Nếu mua 1 lon thì không giảm giá.
- Nếu mua 2 lon thì lon thứ hai được giảm 500 đồng
- Nếu mua 3 lon thì lon thứ hai được giảm 500 đồng và lon thứ ba được giảm giá 10%.
- Nếu mua trên 3 lon thì lon thứ hai được giảm 500 đồng, lon thứ ba được giảm 10% và những lon thứ tư trở đi đều được giảm thêm 2% trên giá đã giảm của lon thứ ba.
a) Hùng mua 3 lon nước tăng lực trên thì phải thanh toán số tiền là bao nhiêu?
b) Vương phải trả 422500 đồng để thanh toán khi mua những lon nước tăng lực trên. Vương đã mua bao nhiêu lon nước?
Câu 6. (1,0 điểm) Tính chiều cao của một ngọn núi (làm tròn đến mét), cho biết tại hai điểm cách nhau \50m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là \(33{}^\circ \) và \(37{}^\circ \).
Câu 7.(1,0 điểm) Trong hình vẽ dưới đây, hai địa điểm A và B cách nhau \(100\text{km}\). Một xe otô khởi hành từ B đến A với vận tốc 40km/h. Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường vuông góc với AB với vận tốc 20km/h. Hỏi sau 90 phút hai xe cách nhau bao xa?
Câu 8.(2,5 điểm) Từ điểm A ở ngoài đường tròn \(\left( O \right)\) \(\left( OA>2R \right)\), vẽ hai tiếp tuyến AB, AC của (O). Gọi K là trung điểm của AC, KB cắt (O) tại D, OA cắt BC tại H.
a) Chứng minh \(HK\,\text{//}\,AB\) và tứ giác CHDK nội tiếp
b) Tia AD cắt (O) tại E. Chứng minh \(K{{C}^{2}}=KD.KB\) và \(BE\,\text{//}\,AC\).
c) Gọi I là giao điểm của BC và AE, tia KI cắt BE tại S. Chứng minh \(BD.BK=2H{{S}^{2}}\).
---(Để xem tiếp nội dung của đề thi số 3 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 4
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS TÂN LẬP- ĐỀ 04
Bài 1. (1,25 điểm) Cho parabol (P): \(y=\frac{1}{2}{{x}^{2}}\) và đường thẳng (d): \(y=x+4\)
a) Vẽ (P) và (d) trên mặt phẳng tọa độ.
b) Xác định tọa độ các giao điểm của (P) và (d) bằng phép tính.
Bài 2. (1,0 điểm) Cho phương trình: \({{x}^{2}}-2mx+2m-1=0\) với x là ẩn số.
a) Chứng tỏ phương trình luôn có nghiệm với mọi giá trị của m.
b) Gọi x1; x2 là hai nghiệm của phương trình. Tìm m sao cho \({{x}_{1}}^{2}+{{x}_{2}}^{2}-3{{x}_{1}}{{x}_{2}}=19\)
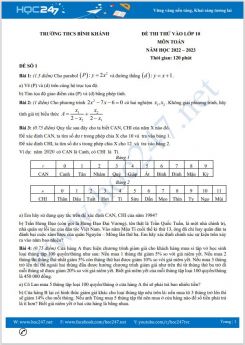
Bài 3. (1,0 điểm) Có hai hãng điện thoại cố định tính phí gọi cho các thuê bao như sau:
|
Hãng |
Thuê bao (ngàn đồng) |
Gọi nội hạt (ngàn đồng/30 phút) |
|
Hãng A |
10 |
6 |
|
Hãng B |
15 |
5 |
Gọi y là giá tiền mà khách hàng phải trả sau x lần 30 phút \(\left( \text{x}\in {{\text{N}}^{\text{*}}} \right)\)
Biết cước phí hàng tháng bằng tổng tiền thuê bao và cước phí gọi nội hạt.
a) Hãy biểu diễn y theo x của từng hãng.
b) Hãy cho biết với cách tính phí như trên thì một khách hàng mỗi tháng gọi bình quân 6 giờ nên sử dụng mạng của hãng nào sẽ rẻ hơn?
Bài 4. (1,0 điểm) Theo dự thảo Luật Thuế tài sản, nhà có giá trị 700 triệu đồng trở lên có thể sẽ bị đánh thuế tài sản ở mức 0,4%. Chẳng hạn, với ngưỡng không chịu thuế là 700 triệu đồng thì một căn nhà có giá trị 800 triệu đồng sẽ bị đánh thuế với phần giá trị 100 triệu đồng, tức 0,4% của 100 triệu đồng.Trường hợp nhà ông A. ở phố Nguyễn Du (Quận Hai Bà Trưng, Hà Nội), diện tích nền là 50m2, nhà 3 tầng. Theo Quyết định 706 của Bộ Xây dựng, nhà 3 tầng có suất đầu tư là 6.810.000 đồng/m2.
a) Như vậy, chi phí xây dựng căn nhà của ông A là bao nhiêu?
b) Mỗi năm nhà ông A. phải nộp thuế nhà là bao nhiêu tiền?
Bài 5. (0,75 điểm) Khuẩn E.Coli thu hút sự quan tâm của các bác sĩ lâm sàng, nhi khoa, vì nó là nguyên nhân của 1/3 số trường hợp tiêu chảy. Việc chẩn đoán gặp khó khăn vì các triệu chứng lâm sàng không đặc hiệu. E.Coli thường có trong nguồn nước. Trong điều kiện thích hợp (khoảng 400C) một con vi khuẩn trong không khí cứ sau 20 phút lại nhân đôi một lần. Giả sử ban đầu có 1 con vi khuẩn. Hỏi sau 6 giờ sẽ sinh ra bao nhiêu con vi khuẩn trong không khí?
Bài 6. (1,0 điểm)
Kính lão đeo mắt của người già thường là loại thấu kính hội tụ. Bạn An đã dùng một chiếc kính lão của ông ngoại để tạo ra hình ảnh của một cây nến trên một tấm màn. Xét cây nến là một vật sáng có hình dạng là đoạn AB đặt vuông góc với trục chính của một thấu kính hội tụ, cách thấu kính một đoạn OA = 4m. Thấu kính có quang tâm O và tiêu điểm F. Vật AB cho ảnh thật A’B’ gấp 3 lần AB. Tính tiêu cự của thấu kính? Biết rằng đường đi của tia sáng được mô tả trong hình vẽ sau:
Bài 7. (1,0 điểm) Muối ăn không chỉ là gia vị mà còn là một vị thuốc quý được dùng để chữa trị nhiều chứng bệnh, các em có biết muối thô được sản xuất như thể nào không?
Ở Việt Nam vùng ven biển miền Trung và miền Nam nghề làm muối dùng phương pháp phơi nước. Người dân thường đào ao rồi thông cho nước biển chảy đầy vào, sau đó đóng lại. Cạnh bên ao thì làm hai cấp sân, thấp dần khoảng 15cm. Mỗi sân đều san phẳng, đắp bờ chia ô vuông vắn; mỗi ô là 4m x10m. Đó là ruộng muối. Khi làm muối thì tát nước từ ao lên sân trên cho đầy. Ruộng trên dùng để tăng nồng độ nước muối. Đợi khoảng năm ngày nắng ráo thì tháo nước mặn cho trút xuống sân dưới, nơi muối bắt đầu kết tinh. Mỗi khi sân dưới gần cạn nước vì nước bốc hơi thì lại châm thêm nước từ ruộng trên xuống ruộng. Cứ châm liên tiếp năm ngày đến khoảng một tháng tùy theo độ ẩm không khí thì nước sẽ cạn và muối đóng thành hột. Người làm muối theo đó gạt muối lên và gánh về. Để vận chuyển muối mà không làm ảnh hưởng đến ruộng những người phụ nữ dùng thúng và đán ông dùng cần xé.
Biết mỗi thúng muối có dạng nửa hình cầu đường kính 45 cm. Cần xé dạng nón cụt chiều cao 50cm, bán kính đáy nhỏ là 40 cm, bán kính đáy lớn là 50cm. Mỗi lần vận chuyển, đàn ông vác một cần xé, phụ nữ gánh hai thúng. Hỏi trong mỗi lần vận chuyển, ai chuyển được nhiều muối hơn (giả sửa muối được gạt ngang miệng cần xé và thúng).
Bài 8. (3,0 điểm) Từ điểm A ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Gọi H là giao điểm của AO và BC. Gọi I trung điểm của AB, Từ B kẻ đường thẳng vuông góc với OI tại K đường thẳng này cắt đường tròn (O) tại D (D khác B).
a) Chứng minh: tứ giác ABOC nội tiếp và OK.OI = OH.OA?
b) Đường tròn (I) đường kính AB cắt AC tại E. Gọi F là giao điểm của BE và OA.
Chứng minh: F đối xứng với O qua H?
c) Chứng minh rằng: đường tròn ngoại tiếp \(\Delta \)AFB đi qua điểm K?
---(Để xem tiếp nội dung của đề thi số 4 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 5
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS TÂN LẬP- ĐỀ 05
Bài 1. (1,25 điểm) Cho (P): y = x2 và (d): y = - x + 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Bài 2. (1,0 điểm) Cho phương trình \({{x}^{2}}-2x-{{m}^{2}}+m=0\)
c) Chứng minh pt luôn có 2 nghiệm phân biệt "m
d) Tìm m để pt có 2 nghiệm x1, x2 thỏa \({{x}_{1}}^{2}+2{{x}_{2}}=4\)
Bài 3. (1,0 điểm) Cửa hàng A nhập chiếc laptop với giá bằng 90% so với cửa hàng B. Cả hai cùng tăng giá bán để đạt mức lợi nhuận là 20% và 15%. Giá bán cửa hàng A thấp hơn cửa hàng B 133000. Tính giá nhập kho của mỗi cửa hàng?
Bài 4. (1,0 điểm) Vệ tinh viễn thông Vinasat-1 của Việt Nam cách mặt đất khoảng 35768km. Tính đường kính vùng phủ sóng tối đa trên mặt đất (xem như cung AB) biết bán kính Trái đất khoảng 6400km.
Bài 5. (0,75 điểm) Ông Hậu khoán số tiền 3,6 triệu đồng để thuê sơn tường nhà ông cho một nhóm thợ. Sau khi người I làm được 7 giờ và người II làm 4 giờ thì họ đã làm được 5/9 công việc. Sau đó họ cùng làm trong 4 giờ thì chỉ còn 1/18 bức tường chưa sơn. Vì hai người này bận công việc khác nên đưa người thứ III làm phần còn lại. Xong việc ông Hậu trả tiền, nhưng cả ba lúng túng không biết phải phân chia thế nào. Ông Hậu nói phải chia theo phần công việc mỗi người đã làm chứ không theo giờ làm được vì năng suất mỗi người không như nhau. Ông Hậu nhờ em tính giúp họ theo hướng đó.
Bài 6. (1,0 điểm) Cứ 4 năm có một năm nhuận 366 ngày vào các năm chia hết cho 4, với các năm có dạng \(\overline{ab00}\) thì năm nhuận khi \(\overline{ab}\) ⋮ 4. Từ năm 1501 đến năm 2019 có bao nhiêu năm nhuận?
Bài 7. (1,0 điểm) Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm \(\widehat{AOB}={{60}^{0}}\) và bán kính đường tròn là 5,1cm?
Bài 8. (3,0 điểm) Cho DABC \(\left( AB < AC \right)\) có ba góc nhọn nội tiếp (O), có 2 đường cao BE và CF cắt nhau tại H. Vẽ đường kính AD của (O). Qua H vẽ đường thẳng d \(\bot\) AD tại K, d cắt AB, AC và BC lần lượt tại M, N và S.
a) Chứng minh: Năm điểm A, E, H, K và F cùng thuộc một đường tròn. Xác định tâm I của đường tròn này?
b) Chứng minh: \(SM.SN=SB.SC\)?
c) Chứng minh: SI \(\bot\) OI?
---(Để xem tiếp nội dung của đề thi số 5 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
Trên đây là một phần trích đoạn nội dung Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Tân Lập. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Mời các em tham khảo tài liệu có liên quan:
- Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Hồ Thị Hương
- Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Phạm Ngọc Thạch
Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.





.JPG?enablejsapi=1)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)