Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Phạm Ngọc Thạch

TRƯỜNG THCS PHẠM NGỌC THẠCH

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2022 – 2023 Thời gian: 120 phút

Bài 1.(1,5 điểm) Cho parabol \(\left( P \right):y=-\frac{1}{2}{{x}^{2}}\) và đường thẳng \(\left( d \right):y=-\frac{1}{2}x-1\) trên cùng một hệ trục tọa độ

a/ Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b/ Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2.(1 điểm) Gọi x₁, x₂ là nghiệm (nếu có) của phương trình x² + 3x – 10 = 0.

Không giải phương trình, hãy tính các biểu thức sau :A =  \(\frac{{{x}_{1}}+2}{{{x}_{2}}}+\frac{{{x}_{2}}+2}{{{x}_{1}}}\)

Bài 3.(0,75 điểm) Nhân ngày “Phụ nữ Việt Nam 20/10”, cửa hàng giỏ xách giảm 30%  cho tất cả các sản phẩm và ai có thẻ “khách hàng thân thiết” sẽ được giảm tiếp 5% trên giá đã giảm.

a/ Hỏi bạn An có thẻ khách hàng thân thiết khi mua một cái túi xách trị giá 500 000 đồng thì phải trả bao nhiêu?

b/ Bạn An mua thêm một cái ví nên phải trả tất cả 693 000 đồng. Hỏi giá ban đầu của cái ví là bao nhiêu?

Bài 4.(0,75 điểm) Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2021, số lượng người xem phim tăng thêm 45% nên tổng doanh thu cũng tăng 8,75%. Hỏi rạp phim đã giảm giá mỗi vé bao nhiêu phần trăm so với giá ban đầu?

Bài 5.( 1 điểm)

Trái bóng Telstar xuất hiện lần đầu tiên ở World Cup 1970 ở Mexico do Adidas sản xuất có đường kính 22,3cm. Trái bóng được may từ 32 múi da đen và trắng.Các múi da màu đen hình ngũ giác đều, các múi da màu trắng hình lục giác đều. Trên bề mặt trái bóng, mỗi múi da màu đen có diện tích 37cm², Mỗi múi da màu trắng có diện tích 55,9cm².

Hãy tính trên trái bóng có bao nhiêu múi da màu đen và màu trắng?

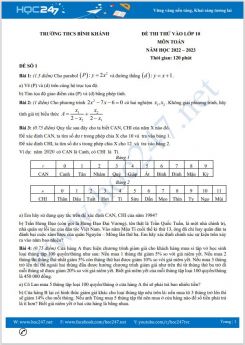
Bài 6.(1 điểm)Giá cước điện thoại di động của một công ty điện thoại trong 1 tháng được tính như sau: tiền thuê bao trả trước 90 000 đồng, Gọi từ 3 000 phút trở xuống không phải trả thêm tiền, trên 3 000 phút thì cứ 1 phút gọi thêm trả 100 đồng mỗi phút. Đồ thị trên hình minh họa thời gian x (phút) gọi thêm và số tiền cước y (đồng) tổng cộng phải trả trong 1 tháng, được xác định bởi công thức y = ax + b.     

a)  Xác định các hệ số a và b.

b)  Nếu gọi thêm 2 000 phút thì tiền cước phải trả trong 1 tháng là bao nhiêu tiền ?

Bài 7.(1 điểm)Quy ước về cách tính năm nhuận:

- Đối với những năm không là năm tròn thế kỷ(có 2 chữ số cuối khác “00”): Nếu năm đó chia hết cho 4 thì là năm nhuận, nếu không chia hết cho 4 thì là không năm nhuận.

- Đối với những năm là năm tròn thế kỷ (có 2 chữ số cuối là “00”): Nếu năm đó chia hết cho 400 thì là năm nhuận, nếu không chia hết cho 400 thì là không năm nhuận.

Ví dụ:  Năm 2019 không là năm nhuận vì 2019 không chia hết cho 4;

Năm 1900 không là năm nhuận vì 1900 là năm tròn thế kỷ nhưng không chia hết cho 400.

Năm 2016 là năm nhuận vì không là năm tròn thế kỷ và chia hết cho 4.

Năm 2000 là năm nhuận vì 2000 chia hết cho 400.

Hỏi:     Năm 2020 là có phải là năm nhuận hay không? Vì sao?

Ngày 20/11/2019 là thứ 4. Hỏi ngày 20/11/2000 là thứ mấy?

Bài 8. (3 điểm) Cho \(\Delta ABC\) nhọn (AB < AC) nội  tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại  H.

a/ Chứng minh: Tứ giác BCEF nội  tiếp. Xác định tâm I của đường tròn  ngoại  tiếp tứ giác này.

b/ Đường thẳng EF cắt  đường thẳng BC tại  M và cắt  đường tròn (O) tại  K và T

( K nằm giữa M và T). Chứng minh: MD.MI = MK.MT

c/ Đường thẳng vuông góc với  HI tại  I cắt  các đường thẳng AB, AC, AD lần lượt tại  N, S, G. Chứng minh: G là trung điểm của đoạn thẳng NS.

ĐÁP ÁN

Bài 1.

a/  Vẽ đúng (P) và (d)                

b/ Tìm đúng tọa độ giao điểm: \(\left( -1;\text{ }-\frac{1}{2} \right)\text{  };\text{  }\left( 2;\text{ }-2 \right)\)    

Bài  2.(1 điểm) Gọi x₁, x₂ là nghiệm (nếu có) của phương trình x² + 3x – 10 = 0.   

 Không giải phương trình, hãy tính các biểu thức sau: A =  \(\frac{{{x}_{1}}+2}{{{x}_{2}}}+\frac{{{x}_{2}}+2}{{{x}_{1}}}\)

\(\Delta ={{b}^{2}}-4ac>0\)

Vậy  phương trình có hai nghiệm phân biệt

Theo hệ thức Vi-ét có \(\left\{ \begin{array}{l}
{x_1} + {x_2} = \frac{{ - b}}{a} = \frac{{ - 3}}{1} =  - 3\\
{x_1}.{x_2} = \frac{c}{a} = \frac{{ - 10}}{1} =  - 10
\end{array} \right.\)

\(\begin{array}{l}
A = \frac{{{x_1} + 2}}{{{x_2}}} + \frac{{{x_2} + 2}}{{{x_1}}} = \frac{{{x_1}^2 + 2{x_1} + {x_2}^2 + 2{x_2}}}{{{x_1}.{x_2}}}\\
A = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}.{x_2} + 2\left( {{x_1} + {x_2}} \right)}}{{{x_1}.{x_2}}} = \\
A = \frac{{{{\left( { - 3} \right)}^2} - 2\left( { - 10} \right) + 2\left( { - 3} \right)}}{{ - 10}} = \frac{{ - 23}}{{10}}
\end{array}\)

---(Để xem tiếp nội dung của đề thi số 1 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS PHẠM NGỌC THẠCH- ĐỀ 02

Câu 1. (1,5 điểm). Cho \(\left( P \right):y=-\frac{1}{2}{{x}^{2}}\) và đường thẳng \(\left( d \right):y=3x+4\).

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Câu 2. (1 điểm). Cho phương trình \({{x}^{2}}+5x-8=0\) có 2 nghiệm là \({{x}_{1}}\), \({{x}_{2}}\). Không giải phương trình, hãy tính giá trị của biểu thức \(C=\frac{{{x}_{1}}}{{{x}_{2}}-2}+\frac{{{x}_{2}}}{{{x}_{1}}-2}\).

Câu 3. (0,75 điểm). Bạn An dự định đem vừa đủ số tiền để mua 20 quyển tập tại nhà sách Nguyễn Văn Cừ. Tuy nhiên, hôm nay nhà sách có chương trình khuyến mãi đầu năm giảm giá 20% mỗi quyển tập. Hỏi với số tiền bạn An đem có thể mua được tất cả bao nhiêu quyển tập?

Câu 4. (0,75 điểm). Hiện tại bạn Bình đã để dành được một số tiền là 800.000.000 đồng. Bạn Bình đang có ý định mua một căn chung cư là 2.000.000.000 đồng. Nên hàng tháng bạn Bình có mức lương 50 triệu đồng một tháng, sau khi trừ chi phí ăn uống, tiền thuê nhà, cho ba mẹ… tổng cộng hết là 30 triệu đồng, số tiền còn lại bạn đều để dành để mua nhà. Gọi m (triệu đồng) là số tiền bạn Bình tiết kiệm được sau t (tháng) (tính luôn cả 800 triệu đã tiết kiệm trước đó).

a) Thiết lập hàm số của m theo t.

b) Hỏi sau bao nhiêu năm kể từ ngày bắt đầu tiết kiệm thì Bình có thể mua được căn chung cư đó?

Câu 5. (1 điểm). Phòng học lớp \(6\text{A}\) gắn máy lạnh. Lớp có \(\text{49}\) học sinh, trong đó có \(\text{40}\) bạn học bán trú. Biết rằng các bạn học bán trú thì đóng tiền điện 100%, các bạn không học bán trú thì đóng \(50%\). Trong tháng \(\text{4}\) lớp đã xài hết \(\text{700 Kwh}\) điện, biết mỗi Kwh điện giá \(\text{2 000}\) đồng. Tính số tiền mỗi học sinh bán trú và không bán trú cần phải đóng (làm tròn đến chữ số hàng nghìn).

Câu 6. (1 điểm). Nhà bạn An có một xô đựng nước có hình dạng hình nón cụt. Đáy xô có đường kính là \(\text{28 cm}\), miệng xô là đáy lớn của hình nó cụt có đường kính là \(\text{36 cm}\). Hỏi nếu cần \(\text{78}\) lít nước thì bạn An phải xách tối thiểu là bao nhiêu lần nếu chiều cao của xô là \(\text{32 cm}\)? 

Câu 7.(1 điểm).  Nhu cầu mua hàng online hiện nay rất lớn. Để vận chuyển các món hàng đó đến tay khách hàng không ai khác chính là các shipper. Ngày \(\text{5/01/2022}\) công ty A cần nhờ các shipper vận chuyển một số hàng. Theo dự định mỗi shipper sẽ vận chuyển 30 món hàng thì sẽ chở hết số hàng trên. Nhưng thực tế mỗi shipper vận chuyển 36 món hàng. Do đó số shipper vận chuyển hàng đó giảm đi 3 người. Tính số hàng mà công ty A đã giao cho khách.

Câu 8.(3 điểm) Cho \(\left( O;R \right)\) và điểm A nằm ngoài \(\left( O \right)\) kẻ hai tiếp tuyến AM, AN (M, N là hai tiếp điểm). Kẻ đường kính MD, AD cắt \(\left( O \right)\) tại K, NK cắt AH tại I.

a) Chứng minh tứ giác ANOM nội tiếp và \(A{{I}^{2}}=IK.IN\).

b) Chứng minh rằng \(\Delta AIM\,\,\#\,\,\Delta MHD\).

c) MI cắt \(\left( O \right)\) tại G. Chứng minh 3 điểm D,H,G thẳng hàng.

---(Để xem tiếp nội dung của đề thi số 2 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS PHẠM NGỌC THẠCH- ĐỀ 03

Câu 1 : (1,5 điểm). Cho hàm số \(y=\frac{-{{x}^{2}}}{4}\) có đồ thị là parabol \(\left( P \right)\) và hàm số \(y=\frac{x}{2}-2\)  có đồ thị là đường thẳng  \(\left( D \right)\)

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( D \right)\) trên cùng một hệ trục toạ độ.

b) Tìm toạ độ các giao điểm của \(\left( P \right)\) và \(\left( D \right)\) bằng phép tính

Câu 2 :  (1 điểm). Gọi \({{x}_{1}}\), \({{x}_{2}}\) là các nghiệm của phương trình \({{x}^{2}}-x-12=0\). Không giải phương trình, tính giá trị của biểu thức \(A=\frac{{{x}_{1}}+1}{{{x}_{2}}}+\frac{{{x}_{2}}+1}{{{x}_{1}}}\).

Câu 3 : (0,75 điểm). Để biết được ngày n tháng t năm 2020 là ngày thứ mất trong tuần. Đầu tiên, đi tính giá trị biểu thức T=n+H, ở đây H được xác định như sau:

Sau đó lấy T chia cho 7 ta được số dư r \(\left( 0\le r\le 6 \right)\)

Nếu r=0 thì ngày đó là ngày thứ Bảy

Nếu r=1 thì ngày đó là ngày Chủ Nhật

Nếu r=2 thì ngày đó là ngày thứ Hai

Nếu r=3 thì ngày đó là ngày thứ Ba

…

Nếu r=6 thì ngày đó là ngày thứ Sáu

a) Hãy sử dụng quy tắc trên để xác định ngày \(30\text{/}04\text{/}2020\) là ngày thứ mấy?

b) Bé An sinh vào tháng \(12\text{/}2020\). Biết rằng ngày sinh của bé An là một bội số của 5 và là Chủ Nhật. Hỏi ngày sinh của bé An là ngày mấy?

Câu 4: (0,75 điểm). Cuối học kì I năm học 2018-2019 lớp 9A có số học sinh giỏi chiếm \(\frac{4}{15}\) học sinh cả lớp, \(\frac{1}{3}\) số học sinh cả lớp là học sinh khá, còn lại 18 em học sinh trung bình. Hỏi cuối học kì I lớp 9A có bao nhiêu học sinh ?

Câu 5: (1 điểm). Người ta nhấn chìm hoàn toàn một tượng đá nhỏ vào một lọ thủy tinh có nước dạng hình trụ; diện tích đáy của lọ thủy tinh là \(9c{{m}^{2}}\) khi đó nước trong lọ dâng cao 4cm. Tính thể tích tượng đá.

Câu 6:  (1 điểm).

Tính chiều cao của một ngọn núi (làm tròn đến mét), cho biết tại hai điểm cách nhau 550m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là \(33{}^\circ \) và \(37{}^\circ \).

Câu 7: (1 điểm). Một vật rơi tự do từ độ cao so với mặt đất là 120 mét. Bỏ qua sức cản không khí, quãng đường chuyển động s (mét) của vật rơi sau thời gian t được biểu diễn gần đúng bởi công thức: \(s=5{{t}^{2}}\), trong đó t là thời gian tính bằng giây.

a) Sau 3 giây vật này cách mặt đất bao nhiêu mét ?

b) Sau bao lâu kể từ khi bắt đầu rơi thì vật này chạm mặt đất ? (Làm tròn kết quả đến chữ số hàng đơn vị)

Câu 8 : (3 điểm) Cho  đường tròn \(\left( O;\,R \right)\) và điểm A nằm ngoài đường tròn \(\left( O \right)\), Vẽ hai tiếp tuyến \(AB,\,AC\) của \(\left( O \right)\) (B,C tiếp điểm). Vẽ cát tuyến \(ADE\) của \(\left( O \right)\)  (D, E thuộc \(\left( O \right)\); D nằm giữa A và E; Tia AD nằm giữa hai tia AB và AO.

a) Chứng minh \(A{{B}^{2}}=AD.AE\).

b) Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp.

c) Đường thẳng AO cắt đường tròn \(\left( O \right)\) tại M và \(N\) (\(M\) nằm giữa A và O). Chứng minh: \(EH.AD=MH.AN\)

---(Để xem tiếp nội dung của đề thi số 3 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS PHẠM NGỌC THẠCH- ĐỀ 04

Câu 1. (2 điểm)

a) Vẽ đồ thị (P) của hàm số \(y=-{{x}^{2}}\) và \(\left( D \right):y=2x-3\) trên cùng một hệ trục tọa độ.

b) Tìm tọa độ các giao điểm của (P) và (D) ở câu trên bằng phép tính.

Câu 2. (1,0 điểm) Vào cuối học kì I, trường trung học cơ sở A có tỉ lệ học sinh xếp loại học lực trung bình trở lên ở khối 7 là 90% học sinh toàn khối 7 và ở khối 9 là 84% học sinh toàn khối 9. Nếu tính chung cả hai khối thì số học sinh xếp loại học lực trung bình trở lên là 864 em, chiếm tỉ lệ 86,4% số học sinh cả khối 7 và khối 9. Hãy cho biết mỗi khối trên có bao nhiêu học sinh?

Câu 3. (2,0 điểm) Bụi mịn hay bụi PM 2.5 là những hạt bụi li ti trong không khí có kích thước
2,5 micromet trở xuống (nhỏ hơn khoảng 30 lần so với sợi tóc người). Loại bụi này hình thành từ các chất như Carbon, Sulfur, Nitrogen và các hợp chất kim loại khác lơ lửng trong không khí. Bụi PM 2.5 có khả năng len sâu vào phổi, đi trực tiếp vào máu và có khả năng gây ra hàng loạt bệnh về ung thư, hô hấp,... Để xác định mức độ bụi PM 2.5 trong không khí người ta thường dùng chỉ số AQI, ví dụ 5AQI, 7AQI. Chỉ số AQI càng lớn thì độ ô nhiễm không khí càng nhiều.

Tại thành phố B, trong tháng 11 vừa qua, người ta đo được mức độ bụi PM 2.5 trong không khí vào lúc 6 giờ sáng là 79 AQI và trung bình mỗi giờ tăng 11 AQI, chỉ giảm đi kể từ 18 giờ cùng ngày.

Gọi y là mức độ bụi PM 2.5 trong không khí của thành phố B, t là số giờ kể từ 6 giờ sáng. Hãy biểu diễn mối liên hệ giữa y và t trong khoảng thời gian từ 6 giờ sáng đến 18 giờ cùng ngày.

b) Tính mức độ bụi PM 2.5 của thành phố B vào lúc 15 giờ.

Câu 4. (1,0 điểm) Quãng đường AB gồm một đoạn lên dốc dài 4km và một đoạn xuống dốc dài 5km. Bạn Tèo đi xe đạp từ A đến B hết 40’ và từ B về A hết 41’ (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.

Câu 5: (1 điểm)   Một mẫu pho mát được cắt ra từ một khối pho mát dạng hình trụ (có các kích thước như trên hình vẽ). Tính theo gam khối lượng của mẫu pho mát biết khối lượng riêng của pho mát là 3g/cm3.

Câu 6. (3,0 điểm) Cho rABC nhọn nội tiếp đường tròn (O) có 3 đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh BFEC, EHDC là các tứ giác nội tiếp.

b) AD cắt (O) tại M. Chứng minh M và H đối xứng nhau qua BC.

c) BE cắt (O) tại N, CF cắt (O) tại K. Chứng minh \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CK}{CF}=4\)

---(Để xem tiếp nội dung của đề thi số 4 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS PHẠM NGỌC THẠCH- ĐỀ 05

Bài 1. (1,5 điểm) Cho parabol (P): y = x2 và đường thẳng (d): y = – \(\frac{1}{2}\)x +1

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2. (1 điểm) Cho phương trình:  \(-2{{x}^{2}}+\frac{1}{2}x+3=0\). Gọi x1, x2 là hai nghiệm (nếu có).

Không giải phương trình, hãy tính giá trị của biểu thức: \(A=\frac{{{x}_{1}}}{{{x}_{2}}}+\frac{{{x}_{2}}}{{{x}_{1}}}-\frac{1}{2}\) 

Bài 3. (1 điểm) Chim cắt là loài chim lớn, có bản tính hung dữ, đặc điểm nổi bật nhất của chúng là đôi mắt rực sáng, bộ móng vuốt và chiếc mỏ sắc như dao nhọn, chúng có khả năng lao nhanh như tên bắn và là nỗi khiếp đảm của không ít các loài chim trời, rắn và những loài thú nhỏ: chuột, thỏ, sóc,…

a. Từ vị trí 16m so với mặt đất, đường bay lên của chim cắt là hàm số được cho bởi công thức sau: y = 30x + 16 (trong đó y là cao độ so với mặt đất, x là thời gian tính bằng giây, \(x\ge 0\)). Hỏi nếu nó muốn bay lên để đậu trên núi cao 256m so với mặt đất thì tốn bao nhiêu giây?

b. Từ vị trí 256m so với mặt đất hãy tìm cao độ khi nó bay xuống sau 3 giây. Biết đường bay xuống của nó được cho bởi công thức: y = – 40x + 256

Bài 4. (0,75 điểm) An, Bình, Cúc vào một cửa hàng mua tập và bút cùng loại.  An mua 20 quyển tập và 4 cây bút hết 176 000 (đồng). Bình mua 2 cây bút và 20 quyển tập hết 168 000 (đồng). Cúc mua 2 cây bút và 1 hộp đựng bút nhưng chỉ trả 36 000 (đồng) do Cúc là khách hàng thân thiết nên được giảm 10% trên tổng số tiền mua. Hỏi 1 hộp đựng bút là bao nhiêu tiền khi không giảm giá?

 Bài 5. (0,75 điểm) Một vận động viên bơi lội khi nhảy ở độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x (tính bằng mét) theo công thức: h = – (x – 1)2 + 4 (xem hình). Hỏi khoảng cách x bằng bao nhiêu:

a) Khi vận động viên ở độ cao 4m?

b) Khi vận động viên chạm mặt nước?

Bài 6.

Khung của nón lá có dạng hình nón được làm bởi các thanh gỗ nối từ đỉnh tới đáy như các đường sinh \(\left( \ell  \right)\), 16 vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn thành những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất to bằng đồng xu.

Đường kính (d = 2r) của chiếc nón lá khoảng 40 (cm);

Chiều cao (h) của chiếc nón lá khoảng 19 (cm)

a. Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vảnh chiếc nón lá.(không kể phần chắp nối, tính gần đúng đến 2 chữ số thập phân, biết \(\pi \) \(\simeq \) 3,14)

b. Tính diện tích phần lá phủ xung quanh của chiếc nón lá. (không kể phần chắp nối, tính gần đúng đến 2 chữ số thập phân). Biết diện tích xung quanh của hình nón là: S = \(\pi \text{ }r\text{ }l\) 

Bài 7. (1 điểm) Bạn Mai đang chuẩn bị bữa điểm tâm gồm đậu phộng nấu và mì xào. Biết rằng cứ mỗi 30 gam đậu phộng nấu chứa 7 gam protein, 30 gam mì xào chứa 3 gam protein. Để bữa ăn có tổng khối lượng 200 gam cung cấp đủ 28 gam protein thì bạn Mai cần bao nhiêu gram mỗi loại?

Bài 8. (3 điểm) Cho đường tròn (O ; R) và điểm A ở ngoài đường tròn với OA > 2R. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là tiếp điểm). Vẽ dây BE của đường tròn (O) song song với AC; AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của đoạn DE.

a) Chứng minh: 5 điểm A, B, C, O, M cùng thuộc một đường tròn và SC² = SE.SD?

b) Tia BM cắt (O) tại K khác B. Chứng minh: tứ giác MKCD là hình bình hành?

c) Hai đường thẳng DE và BC cắt nhau tại V, đường thẳng SV cắt BE tại H. Chứng minh: Ba điểm  H, O, C thẳng hàng?

---(Để xem tiếp nội dung của đề thi số 5 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

Trên đây là một phần trích đoạn nội dung Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Phạm Ngọc Thạch. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.