Bộ 5 đề thi HK1 môn Toán 12 năm 2022-2023 có đáp án Trường THPT Nguyễn Trãi

TRƯỜNG THPT NGUYỄN TRÃI

ĐỀ THI HỌC KÌ 1 NĂM HỌC 2022 – 2023 MÔN: TOÁN 12 Thời gian làm bài: 60 phút

Câu 1. Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. \(\left( 0;1 \right)\).                   

B. \(\left( -1;0 \right)\).               

C. \(\left( 1;+\infty  \right)\).             

D. \(\left( -1;1 \right)\).

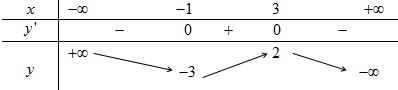
Câu 2. Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên là:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.\(\left( -1;3 \right)\).          

B. \(\left( -3;2 \right)\). 

C. \(\left( -\infty ;-1 \right)\).   

D.\(\left( 3;+\infty  \right)\).

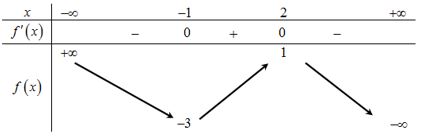
Câu 3. Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:

Giá trị cực đại của hàm số đã cho là

A.  -1.          

B. 2.           

C. 1.    

D. -3.

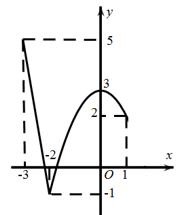
Câu 4.Cho hàm số \(y=f(x)\) liên tục trên đoạn \(\left[ -3;1 \right]\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ -3;1 \right]\). Giá trị của \(M-m\) bằng

A. 6.   

B. 2.              

C. 8.    

D. 4.

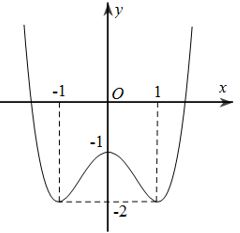
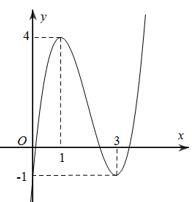
Câu 5. Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ

Điểm cực đại của đồ thị hàm số đã cho là

A. \(\left( 3;-1 \right)\).           

B. \(\left( -1;3 \right)\). 

C. \(\left( 4;1 \right)\).    

D. \(\left( 1;4 \right)\).

Câu 6. Đồ thị hàm số \(y=\frac{2x-1}{x+3}\) có một đường tiệm cận đứng là

A. x=3.

B. y=2.         

C. x=-3.     

D. y=-2.

Câu 7.  Cho \(a\) là số thực dương tùy ý, \(\frac{{{a}^{\frac{2}{3}}}.{{a}^{\frac{3}{4}}}}{\sqrt[6]{a}}\) bằng

A. \({{a}^{\frac{1}{3}}}\).        

B. \({{a}^{\frac{5}{4}}}\).                

C. \({{a}^{\frac{3}{4}}}\).        

D. \({{a}^{\frac{4}{5}}}\).

Câu 8. Tập xác định của hàm số \(y={{\left( 3x-1 \right)}^{-4}}\) là

A. \(\left( \frac{1}{3};+\infty  \right)\).               

B. \(\left( -\infty ;\frac{1}{3} \right)\).                 

C. \(\mathbb{R}\).          

D. \(\mathbb{R}\backslash \left\{ \frac{1}{3} \right\}\)

Câu 9. Tập xác định của hàm số \(y=\ln \left( 2x-1 \right)\) là

A. \(\left[ \frac{1}{2};+\infty  \right)\).                 

B. \(\left( -\infty ;\frac{1}{2} \right)\).

C. \(\left( \frac{1}{2};+\infty  \right)\).           

D. \(\left( -\infty ;\frac{1}{2} \right]\). 

Câu 10. Hình đa diện dưới đây gồm bao nhiêu mặt

A. 13   

B. 8            

C. 11    

D. 9

......

---(Để xem tiếp nội dung của đề thi số 1 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI HK1 MÔN TOÁN 12 NĂM 2022-2023 TRƯỜNG THPT NGUYỄN TRÃI - ĐỀ 02

Câu 1: Đồ thị hàm số \(y=\frac{2x-1}{x-3}\) có bao nhiêu đường tiệm cận?

A. 0.                  

B. 1.              

C. 2.              

D. 3.

Câu 2: Phương trình \({{3.2}^{x}}-{{4}^{x}}-2=0\) có 2 nghiệm \({{x}_{1}}\), \({{x}_{2}}\). Tính tổng \({{x}_{1}}+{{x}_{2}}\).

A. 4.                

B. 2.              

C. 1.         

D. 3. 

Câu 3: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính theo a thể tích V của khối chóp S.ABC.

A. \(V=\frac{{{a}^{3}}\sqrt{3}}{24}\).                        

B. \(V=\frac{{{a}^{3}}\sqrt{3}}{3}\).          

C. \(V=\frac{{{a}^{3}}\sqrt{3}}{12}\).                             

D. \(V=\frac{{{a}^{3}}}{12}\).

Câu 4: Trong các hàm số sau, hàm số nào nghịch biến trên $\mathbb{R}$ ?

A. \(y={{\log }_{\frac{1}{2}}}x\).          

B. \(y={{\log }_{5}}x\).   

C. \(y={{\left( \frac{2}{3} \right)}^{-x}}\).           

D. \(y={{\left( \frac{e}{3} \right)}^{x}}\).

Câu 5: Hình nón có bán kính đáy, chiều cao, đường sinh lần lượt là r, h, l. Diện tích xung quanh của hình nón là:

A. \(S=\pi rl\).                      

B. \(S=\pi hl\).                  

C. \(S=\pi {{r}^{2}}\).   

D. \(S=\pi rh\).

Câu 6: Tập nghiệm của bất phương trình \({{\log }_{\frac{1}{3}}}({{x}^{2}}-8x+15)>-1\) là

A. \(\left( 2;3 \right)\cup \left( 5;6 \right)\).              

B. \(\varnothing \).        

C. (2; 6).  

D. \(\mathbb{R}\). 

Câu 7: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng \(\left( -1;\ +\infty  \right)\).         

B. Hàm số đồng biến trên khoảng \(\left( -\infty ;\ 1 \right)\).

C. Hàm số nghịch biến trên khoảng \(\left( -1;\ 3 \right)\).    

D. Hàm số nghịch biến trên khoảng \(\left( -1;\ 1 \right)\).

Câu 8: Tập nghiệm của bất phương trình \({{\left( \frac{3}{4} \right)}^{-{{x}^{2}}}}>\frac{81}{256}\)

A. \(\left( -\infty ;-2 \right)\).                                      

B. \(\mathbb{R}\).          

C. \(\left( -\infty ;-2 \right)\cup \left( 2;+\infty  \right)\).                          

D. \(\left( -2;2 \right)\).

Câu 9: Hàm số \(y=\frac{2x-1}{-3+3x}\) có tiệm cận ngang là

A. \(y=\frac{2}{3}\).            

B. \(x=\frac{2}{3}\).       

C. \(y=1\).                         

D. \(y=-\frac{2}{3}\).

Câu 10: Bảng biến thiên dưới đây là của hàm số nào?

A. \(y=\frac{x+1}{x-2}\).     

B. \(y=\frac{x-1}{2x+2}\).                                       

C. \(y=\frac{x+3}{2+x}\).    

D. \(y=\frac{2x+1}{x-2}\).

......

---(Để xem tiếp nội dung của đề thi số 2 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI HK1 MÔN TOÁN 12 NĂM 2022-2023 TRƯỜNG THPT NGUYỄN TRÃI - ĐỀ 03

Câu 1 (TH). Cho hàm số \(y=f\left( x \right)={{x}^{4}}+2018.\)_ Điểm cực tiểu của hàm số là

A. 2018                            

B. 2019                            

C. 1                                  

D. 0

Câu 2 (VD). Tìm tất cả các giá trị thực của tham số m để hàm số \(y={{x}^{3}}-2m{{x}^{2}}+{{m}^{2}}x+3\) đạt cực đại tại x=1

A. m=3                          

B. m=1, m=3                 

C. m=1                         

D. Không tồn tại m

Câu 3 (NB). Nghiệm của phương trình \({{3}^{x}}=6\) là

A. \({{\log }_{3}}2\)       

B. 2                                  

C. \({{\log }_{3}}6\)       

D. \({{\log }_{6}}3\)

Câu 4 (TH). Đồ thị dưới là đồ thị của hàm số nào sau đây?

A. \(y={{x}^{4}}+3{{x}^{2}}-2\)                           

B. \(y={{x}^{4}}-2x-2\)   

C. \(y={{x}^{4}}-3{{x}^{2}}-2\)                   

D. \(y={{x}^{4}}+2{{x}^{2}}-1\)

Câu 5 (TH). Tính đạo hàm của hàm số \(y={{3}^{{{x}^{2}}}}\)

A. \({y}'=2x{{.3}^{{{x}^{2}}}}.\ln 3\)                   

B. \({y}'={{x}^{2}}{{.3}^{{{x}^{2}}-1}}\)        

C. \({y}'={{3}^{{{x}^{2}}}}\ln 3\)                                 

D. \({y}'=2x{{.3}^{{{x}^{2}}}}\)

Câu 6 (TH). Cho khối lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có diện tích đáy bằng \({{a}^{2}}\), mặt bên \(AB{B}'{A}'\) là hình vuông có \(A{B}'=b\sqrt{2}.\) Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) là

A. \(\frac{{{a}^{2}}b}{3}\)                                  

B. \(2{{a}^{2}}b\)

C. \(3{{a}^{2}}b\)         

D. \({{a}^{2}}b\)

Câu 7 (TH). Nếu \({{\log }_{a}}b=4\) thì \({{\log }_{\sqrt{a}}}{{b}^{2}}+{{\log }_{a}}\left( ab \right)\) bằng

A. 9                                  

B. 21                                

C. 20                                

D. 13

Câu 8 (VD). Cho hàm số \(y=\ln \left( {{e}^{x}}+1 \right)-\frac{x}{2}.\) Khi đó nghiệm của phương trình \({y}'=\frac{1}{4}\) là

A. \({{\log }_{3}}e\)         

B. \(\frac{3}{e}\)              

C. \(\ln 3\)                 

D. \(\ln 2\)

Câu 9 (TH). Trong không gian cho tam giác OIM vuông tại I, \(IOM=30{}^\circ \) và IM=a. Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay có diện tích toàn phần là

A. \(\pi {{a}^{2}}\)        

B. \(4\pi {{a}^{2}}\)         

C. \(2\pi {{a}^{2}}\)         

D. \(3\pi {{a}^{2}}\)

Câu 10 (VD). Một hình trụ \(\left( T \right)\) có hai đáy là hai hình tròn \(\left( O;r \right)\) và \(\left( {O}';r \right)\). Khoảng cách giữa hai đáy là \(O{O}'=a\sqrt{3}.\) Một hình nón \(\left( N \right)\) có đỉnh là \({O}'\) và đáy là hình tròn \(\left( O;r \right)\). Gọi \({{S}_{1}},{{S}_{2}}\) lần lượt là diện tích xung quanh của \(\left( T \right)\) và \(\left( N \right).\) Khi đó tỉ số \(\frac{{{S}_{1}}}{{{S}_{2}}}\) bằng

A. \(\frac{1}{\sqrt{3}}\)  

B. 1                                  

C. 2                                  

D. \(\sqrt{3}\)

......

---(Để xem tiếp nội dung của đề thi số 3 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI HK1 MÔN TOÁN 12 NĂM 2022-2023 TRƯỜNG THPT NGUYỄN TRÃI - ĐỀ 04

Câu 1. Cho biểu thức \(K=\sqrt[{}]{2\sqrt[3]{2}}\). Hãy tìm biểu thức K được viết dưới dạng lũy thừa với số mũ hữu tỉ.

A. \(K={{2}^{\frac{5}{3}}}\)                         

B. \(K={{2}^{\frac{2}{3}}}\)                       

C. \(K={{2}^{\frac{4}{3}}}\)               

D. \(K={{2}^{\frac{1}{3}}}\)

Câu 2. Tìm tất cả các giá trị thực của a để biểu thức \(B=lo{{g}_{2}}\left( a-7 \right)\) có nghĩa.

A. \(a > 7\)                          

B. \(a\le 7\)                                

C. \(a\le 7\)      

D. \(a<7\)

Câu 3. Cho \(0 < a \ne 1\). Tính giá trị của biểu thức \({{a}^{3{{\log }_{a}}\sqrt{2}}}\).

A. \(2\sqrt{2}\)                           

B. \(3\sqrt{2}\)                       

C. \(2\sqrt{3}\)                         

D. \(\sqrt{2}\) 

Câu 4. Tìm tất cả các giá trị của m để phương trình \({{8}^{2{{x}^{2}}-2\text{x}-4}}+{{m}^{2}}-m=0\) có nghiệm.

A. \(m<0\).                          

B. \(0 < m < 1.\)

C. \(m<0\vee m>1\).                  

D. \(m>1\).

Câu 5. Tìm tập nghiệm của phương trình: \({{5}^{-4x-2}}={{125}^{4x}}\).

A. \(\left\{ \frac{1}{2} \right\}\)                          

B. \(\left\{ 2 \right\}\)            

C. \(\left\{ -\frac{1}{8} \right\}\)                              

D. \(\left\{ -\frac{1}{16} \right\}\)

Câu 6. Tìm tập nghiệm của phương trình: \({{5}^{{{x}^{2}}+3x-10}}=1\).

A. \(\left\{ 1;2 \right\}\)                        

B. \(\left\{ -5;2 \right\}\)                      

C. \(\left\{ -5;-2 \right\}\)           

D. \(\left\{ 2;5 \right\}\)

Câu 7. Tìm tập nghiệm của phương trình: \({{(\sqrt{2}-1)}^{2x}}=\sqrt{2}+1\).

A. \(\left\{ -1 \right\}\)                             

B. \(\left\{ 1 \right\}\)                        

C. \(\left\{ -\frac{1}{2} \right\}\)                            

D. \(\left\{ {\frac{1}{2}} \right\}\)

Câu 8. Tìm tập nghiệm của phương trình: \({3^{2x}}{.2^{2x + 1}} = 72\)

A. \(\left\{ {\frac{1}{4}} \right\}\)                               

B. \(\left\{ { - \frac{3}{4}} \right\}\)                     

C. \(\left\{ { - 1} \right\}\)                          

D. \(\left\{ 1 \right\}\)  

Câu 9. \(J = \int {x{e^{{x^2} + 1}}dx} \)  bằng:

A. \(J = 2x{e^{{x^2} + 1}} + C\) 

B. \(J = {e^{{x^2} + 1}} + C\)           

C. \(J = {x^2}{e^{{x^2} + 1}} + C\) 

D. \(J = \frac{1}{2}{e^{{x^2} + 1}} + C\) 

Câu 10. Tìm nguyên hàm của hàm số \(f(x) = {e^x} - {e^{ - x}}\) 

A. \(\int {f(x)} dx = {e^x} + {e^{ - x}} + C\)                                      

B. \(\int {f(x)} dx =  - {e^x} + {e^{ - x}} + C\) 

C. \(\int {f(x)} dx = {e^x} - {e^{ - x}} + C\)                                     

D. \(\int {f(x)} dx =  - {e^x} - {e^{ - x}} + C\)

......

---(Để xem tiếp nội dung của đề thi số 4 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI HK1 MÔN TOÁN 12 NĂM 2022-2023 TRƯỜNG THPT NGUYỄN TRÃI - ĐỀ 05

 

Câu 1: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình dưới đây.

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{1}{2f\left( x \right)-1}\) là

A. 3                           

B. 0                            

C. 2                             

D. 1

Câu 2: Đồ thị như hình vẽ là đồ thị của hàm số nào dưới đây?

A. \(y={{x}^{3}}-\text{3}{{x}^{2}}-4\).                 

B. \(y=-{{x}^{3}}-\text{3}{{x}^{2}}-4.\)                    

C. \(y=-{{x}^{3}}\text{+3}{{x}^{2}}-4\).               

D. \(y={{x}^{3}}-\text{3}{{x}^{2}}+4\).

Câu 3: Tìm tất cả các giá trị thực của tham số m để hàm số \(y={{x}^{4}}+\left( m-1 \right){{x}^{2}}+{{m}^{2}}\) đạt cực tiểu tại x=0

A. \(m\le 1\).                    

B. \(m\ge 1\).                   

C. \(m=1\).                       

D. \(m\in \mathbb{R}\).

Câu 4: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:

Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên \(\left( -\infty ;0 \right)\cup \left( 1;+\infty  \right)\).

B. Hàm số nghịch biến trên \(\left( -\infty ;1 \right)\).

C. Hàm số đồng biến trên \(\left( 0;1 \right)\).                           

D. Hàm số đồng biến trên \(\left( -\infty ;2 \right)\).

Câu 5: Đồ thị hàm số \(y=\frac{\sqrt{x-3}}{{{x}^{2}}+x-6}\) có bao nhiêu đường tiệm cận?

A. 2.                                 

B. 0.                                 

C. 3.                                 

D. 1.

Câu 6: Cho hàm số \(y=\frac{8x-5}{x+3}\). Kết luận nào sau đây đúng?

A. Hàm số đồng biến trên khoảng \(\left( -\infty ;-3 \right)\cup \left( -3;+\infty  \right)\).

B. Hàm số luôn đồng biến trên từng khoảng xác định của nó.

C. Hàm số luôn đồng biến trên $\mathbb{R}$.

D. Hàm số nghịch biến trên khoảng $\left( 0;2 \right)$.

Câu 7: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau

Đồ thị của hàm số \(y=\left| f\left( x \right) \right|\) có bao nhiêu điểm cực trị?

A. 3                            

B. 4                              

C. 5                             

D. 2

Câu 8: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình bên. Phát biểu nào sau đây là đúng?

A. Hàm số có 3 cực trị                                          .       

B. Hàm số đạt cực tiểu tại x=1.

C. Giá trị cực tiểu của hàm số là -1.                               

D. Hàm số đạt cực đại tại x=1.

Câu 9: Cho các số thực \(a,b,\alpha \left( a>b>0,\alpha \ne 1 \right)\). Mệnh đề nào sau đây đúng?

A. \({{\left( a-b \right)}^{\alpha }}={{a}^{\alpha }}-{{b}^{\alpha }}\). 

B. \({{\left( ab \right)}^{\alpha }}={{a}^{\alpha }}.{{b}^{\alpha }}.\)            

C. \({{\left( a+b \right)}^{\alpha }}={{a}^{\alpha }}+{{b}^{\alpha }}.\)              

D. \({{\left( \frac{a}{b} \right)}^{\alpha }}=\frac{{{a}^{\alpha }}}{{{b}^{-\alpha }}}.\)

Câu 10: Cho hàm số \(y=\frac{x+1}{{{x}^{2}}-2mx+4}\). Tìm tất cả các giá trị của tham số m để đồ thị có ba đường tiệm cận

A. m > 2  

B. \(\left[ \begin{array}{l}
m > 2\\
m <  - 2
\end{array} \right.\).           

C. \(\left\{ \begin{array}{l}
m <  - 2\\
m \ne  - \frac{5}{2}
\end{array} \right.\)       

D. \(\left[ \begin{array}{l}
m > 2\\
\left\{ \begin{array}{l}
m <  - 2\\
m \ne  - \frac{5}{2}
\end{array} \right.
\end{array} \right.\) 

......

---(Để xem tiếp nội dung của đề thi số 5 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

Trên đây là một phần nội dung Bộ 5 đề thi HK1 môn Toán 12 năm 2022-2023 có đáp án Trường THPT Nguyễn Trãi. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Mời các em tham khảo tài liệu có liên quan:

• Bộ 5 đề thi HK1 môn Toán 12 năm 2022-2023 có đáp án Trường THPT Gia Định
• Bộ 5 đề thi HK1 môn Toán 12 năm 2022-2023 có đáp án Trường THPT Nguyễn Thượng Hiền

Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.