Bài tập 40 trang 162 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:  

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

+) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi. 

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

Lời giải chi tiết

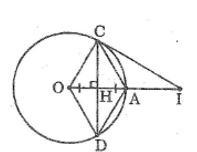
\(a)\) Gọi \(H\) là giao điểm của \(OA\) và \(CD\)

Vì \(CD\) là đường trung trực của \(OA\) nên:

    \(CD ⊥ OA\) và \(HA = HO\)

Xét đường tròn (O) có \(CD ⊥ OA\) tại H nên H là trung điểm của dây CD hay \(HC = HD\) (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Vì tứ giác \(ACOD\) có hai đường chéo CD và OA cắt nhau tại trung điểm H của mỗi đường nên nó là hình bình hành.

Đồng thời \(CD ⊥ OA\) nên \(ACOD\) là hình thoi.

\(b)\) Vì \(ACOD\) là hình thoi nên \(AC = OC\)

Mà \(OC = OA ( = R)\) nên \(OA=OC=AC\), suy ra tam giác \(OAC\) đều.

Suy ra: \(\widehat {COA} = 60^\circ \) hay \(\widehat {COI} = 60^\circ \)

Mà \(CI ⊥ OC\) (tính chất tiếp tuyến)

Trong tam giác vuông \(OCI,\) ta có:

\(CI = OC.\tan\widehat {COI} \)\(= R.\tan60^\circ  = R\sqrt 3 \).

-- Mod Toán 9 HỌC247