Bài tập 2.17 trang 110 SBT Toán 9 Tập 1
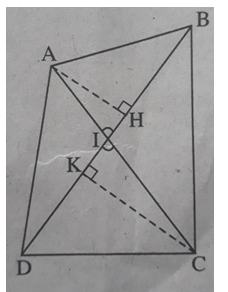
Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng SABCD = \(\frac{1}{2}\) AC.BD.sinα.
Hướng dẫn giải chi tiết
Giả sử hai đường chéo AC, BD cắt nhau tại I, (AIB) ̂ = α là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sinα, CK = CI.sinα,
Diện tích tam giác ABD là SABD = \(\frac{1}{2}\) BD.AH.
Diện tích tam giác CBD là SCBD = \(\frac{1}{2}\) BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = SABD + SCBD = \(\frac{1}{2}\)BD.(AH + CK)
= \(\frac{1}{2}\) BD.(AI + CI)sinα = \(\frac{1}{2}\)BD.AC.sinα
-- Mod Toán 9 HỌC247
-


Bài 2.22 trang 111 sách bài tập toán 9 tập 1
bởi Spider man
 01/10/2018
01/10/2018
Bài 2.22 - Bài tập bổ sung (Sách bài tập trang 111)
Các cạnh của một hình chữ nhật bằng \(3cm\) và \(\sqrt{3}cm\). Hãy tìm các góc hợp bởi đường chéo và các cạnh của hình chữ nhật đó ?
Theo dõi (0) 1 Trả lời -


Bài 2.21 trang 111 sách bài tập toán 9 tập 1
bởi Lê Nhật Minh
 01/10/2018
01/10/2018
Bài 2.21 - Bài tập bổ sung (Sách bài tập trang 111)
Tính các góc của một hình thoi, biết hai đường chéo của nó có độ dài là \(2\sqrt{3}\) và \(2\) ?
Theo dõi (0) 1 Trả lời -


Bài 2.20 trang 110 sách bài tập toán 9 tập 1
bởi thu hằng
 01/10/2018
01/10/2018
Bài 2.20 - Bài tập bổ sung (Sách bài tập trang 110)
Trong hình thang vuông ABCD với các đáy là AD, BC có \(\widehat{A}=\widehat{B}=90^0;\widehat{ACD}=90^0;BC=4cm;AD=16cm\). Hãy tìm các góc C và D của hình thang ?
Theo dõi (0) 1 Trả lời -


Bài 2.19 trang 110 sách bài tập toán 9 tập 1
bởi Nguyễn Thanh Thảo
 01/10/2018
01/10/2018
Bài 2.19 - Bài tập bổ sung (Sách bài tập trang 110)
Tính giá trị biểu thức :
a) \(\dfrac{3cotg60^0}{2\cos^230^0-1}\)
b) \(\dfrac{\cos60^0}{1+\sin60^0}+\dfrac{1}{tg30^0}\)
Theo dõi (0) 1 Trả lời -


Bài 2.18 trang 110 sách bài tập toán 9 tập 1
bởi Nguyen Ngoc
 26/09/2018
26/09/2018
Bài 2.18 - Bài tập bổ sung (Sách bài tập trang 110)
Cho góc nhọn \(\alpha\) :
a) Chứng minh rằng :
\(\dfrac{1-tg\alpha}{1+tg\alpha}=\dfrac{\cos\alpha-\sin\alpha}{\cos\alpha+\sin\alpha}\)
b) Cho \(tg\alpha=\dfrac{1}{3}\). Tính :
\(\dfrac{\cos\alpha-\sin\alpha}{\cos\alpha+\sin\alpha}\)
Theo dõi (0) 1 Trả lời